Queso: Episodio 0

Seguimos trabajando en crear un laboratorio de puertas abiertas, donde puedas ver la cocina de lo que luego se transforma en papers y publicaciones como Thor, Ramen y el CONICET mandan. En esta segunda entrega de Diarios de Investigación, nos toca compartir los primeros resultados del experimento “Queso” en el que más de 18 mil personas respondieron 23 preguntas relacionadas con la matemática: desde cuentas simples hasta rotación mental de objetos en el espacio.

Si no hiciste el test, podés tomarte los 5 a 10 minutos que lleva y hacerlo acá. Tu participación nos ayuda mucho y también suma un montón que lo compartas en tus redes sociales. ¡Spoiler alert! Para los nuevos participantes hicimos una pequeña modificación que te vamos a contar al final de este texto.

Ahora sí, lo adeudado: ¿Qué buscábamos y qué estamos empezando a ver en esta maraña de datos?

Somos multitud

Lo primero que queremos compartir es que el experimento fue un éxito absoluto. En una semana, 18K+ personas respondieron por lo menos a una de las preguntas del cuestionario y 15K+respondieron las 23. Esto es impresionante. No lo esperábamos. Gracias por el aguante.

Ideas nuevas

Semejante cantidad de participantes (dos órdenes de magnitud por encima de la cantidad que se suele encontrar en los experimentos habituales de cognición matemática) nos permitió observar cosas recontra interesantes. Creemos que varias de ellas son novedosas (y, probablemente, serán materia prima para publicar varios papers) pero no queremos dejar de mencionar algo que nos parece súper importante: parte de este ejercicio consiste en encontrarnos con ideas que no se nos habían ocurrido cuando lo pensamos. Acá es donde entran ustedes.

Tenemos el privilegio de ser leídos por personas activamente interesadas en ciencia que pueden aportar mucho: docentes, científicas, desarrolladores, estadísticas y curiosos en general. Es muy probable que, luego de leer estos resultados, se les ocurran nuevas propuestas o críticas constructivas. Por eso hacemos estos Diarios. Para que todos aquellos que tengan ideas las compartan con nosotros a medida que progresamos hacia un reporte científico en revistas indexadas. Así, vamos a poder hacer un mejor trabajo colectivo.

Las preguntas

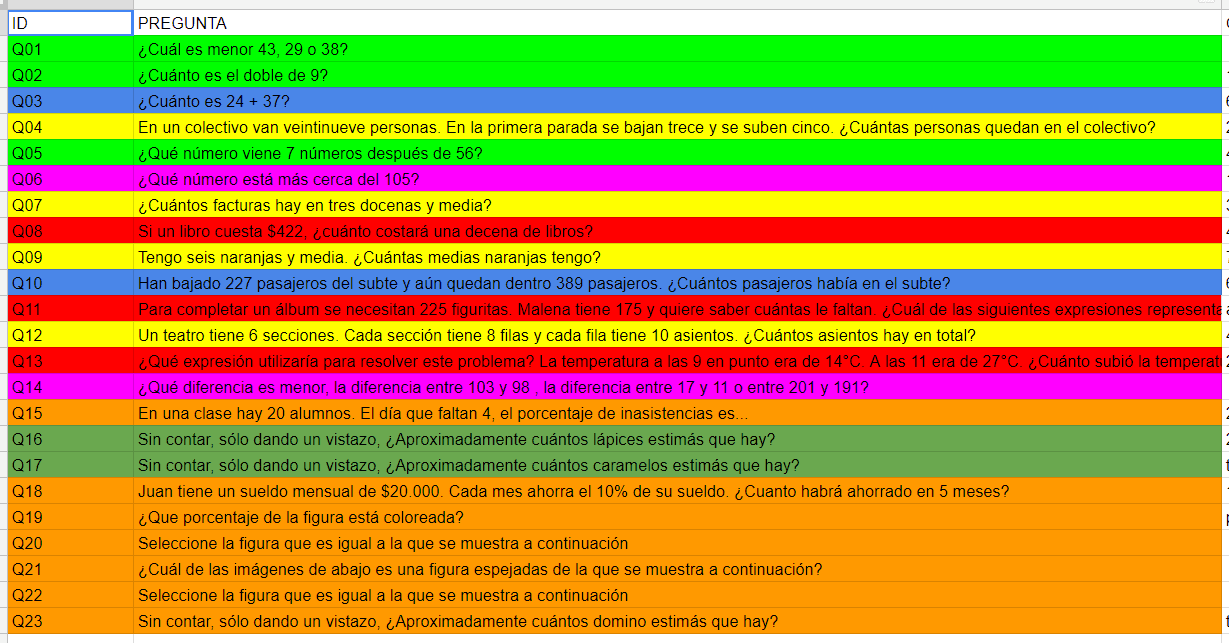
En la imagen de abajo pueden encontrar las 23 preguntas que hicimos. Ténganlas a mano para entender mejor de qué estamos hablando en cada momento. Están coloreadas de una manera particular y ahora se van a enterar el porqué.

Última aclaración antes de que ir a los resultados: es posible que alguno se pierda cuando hablemos de conceptos como regresiones simples o múltiples. A no desanimar, a nosotros en nuestras reuniones internas nos pasa siempre que alguno sabe más o menos de un tema. Es cuestión de seguir leyendo que, por contexto y un poco de ósmosis, van a entender las ideas principales.

¿Listos? ¡Vamos!

Los resultados

Datos generales y demográficos

Analizamos los datos de 18.098 participantes, de los cuales 15.187 contestaron las 23 preguntas.

Entre quienes contestaron todas las preguntas, obtuvimos las siguientes tasas de acierto para cada una de ellas:

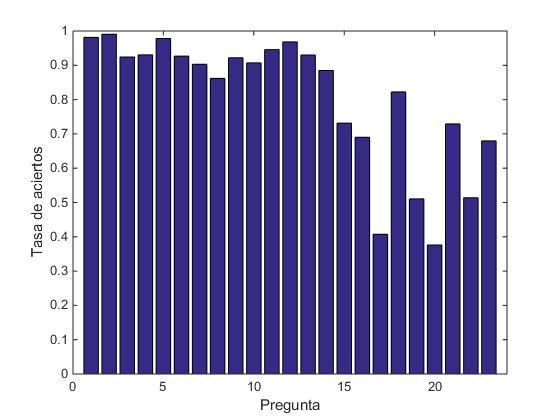
Creemos que la disminución en la tasa de aciertos para las últimas preguntas se debe, probablemente, a dos factores: esas preguntas eran las más difíciles y aparece el cansancio natural luego de varios ejercicios.

También vemos tendencias esperadas para la cantidad de respuestas correctas en función del nivel educativo y de la edad:

La cantidad de respuestas correctas promedio pasa de ~17 para quienes tienen educación primaria a ~19 para quienes tienen posgrado. A su vez, pasa de ~17.5 para las personas de 18 años, a ~19 para las de 35. Luego, a partir de los ~35, parece disminuir lentamente la cantidad de correctas con una caída más abrupta a partir de los 55 años. Solo consideramos en este análisis edades para las cuales teníamos por lo menos 20 participantes de esa edad.

Regresiones simples

Corrimos regresiones simples, con una variable dependiente y una independiente, como una forma de estudiar el poder predictivo de unas respuestas sobre otras.

Para cada una de las 23 preguntas, corrimos 22 regresiones simples tomando como variable independiente la respuesta (correcta o incorrecta) a cada una de las otras 22 preguntas y como variable dependiente la respuesta a la pregunta en cuestión (también, correcta o incorrecta; las dos variables de la regresión son binarias). Solo consideramos como significativas las regresiones con p<0.005.

La pendiente de cada una de estas regresiones nos informa cuánto cambia la probabilidad de haber acertado una respuesta si alguien acertó o no otra. Son estos valores, los de las pendientes de las regresiones, los que empezamos a analizar.

Aclaración que pueden saltear y pasar al próximo párrafo: es interesante observar que estas pendientes no son iguales si intercambiamos la variable dependiente y la independiente (porque medimos una relación direccional, si hubiesemos medido, por ejemplo, la correlación entre las respuestas a dos preguntas, sí observaríamos esa simetría). Por ejemplo, supongamos que preguntamos cuánto es 7 x 14 y la mitad de las personas contestaron bien. En otra pregunta pedimos algo bastante más difícil: 789 x 14. De la mitad que contestó bien 7×14, solo 2% contestó bien 789×14. La mitad que contestó 7×14 mal, también contestó mal la más difícil. O sea que la probabilidad de haber contestado bien 789×14 aumentó de 0 a 2% si hice bien 7×14 en relación a si la hice mal. Sin embargo, la probabilidad de haber contestado bien 7×14 si hice bien 789×14 (para este grupo de participantes) es de 100%. Si hice mal 789×14, eso no me dice mucho sobre cómo me fue con 7×14. De hecho, la probabilidad de haber acertado pasa a ser apenas mayor a 50% (recordando que 50% contestó bien 7×14). Entonces, la probabilidad de acertar 7×14 pasa de casi 50% a 100% según haya acertado o no 789×14.

El problema es que ahora teníamos una tabla preciosa con las relaciones predictivas entre las preguntas que lucía así:

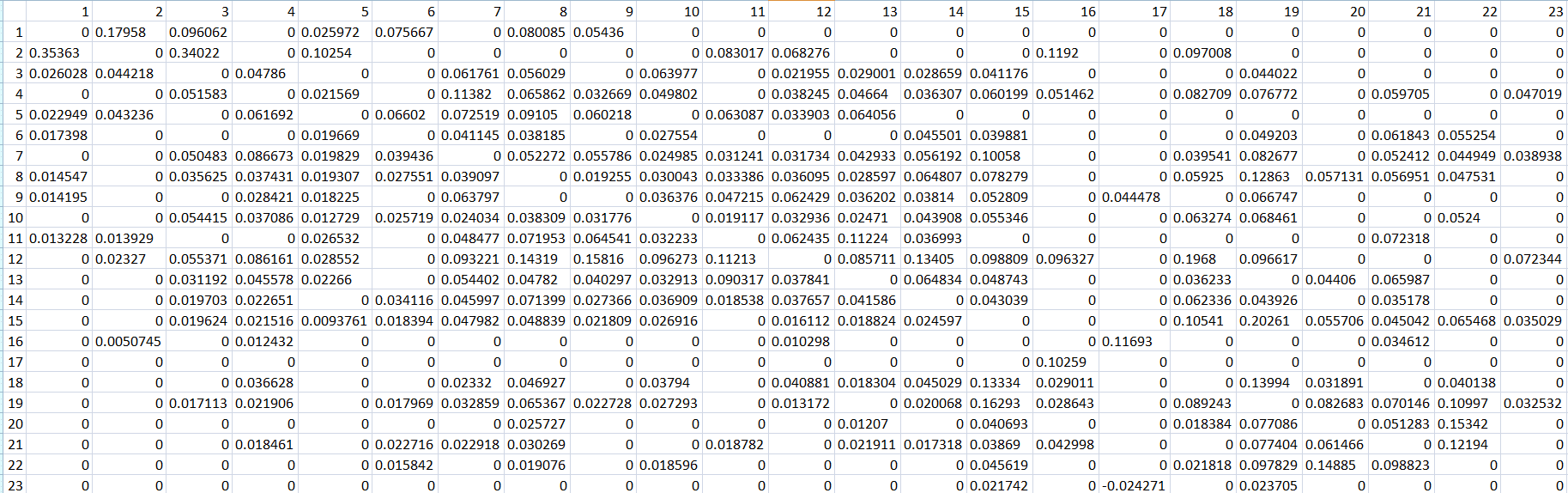
AHPEROQUÉINFORMATIVAYFÁCILDELEERESTAMATRIZ

Tener los datos ordenados y visibles de esta manera nos daba un montón de ventajas como, por ejemplo, poder decir que no entendíamos nada, dejar el análisis y pedir empanadas.

Amor por la visualización de datos mediante (?), se nos ocurrió usar cada pregunta como un nodo y cada relación entre preguntas como una arista, lo que nos permite pensar estas relaciones y visualizarlas en forma de grafo.

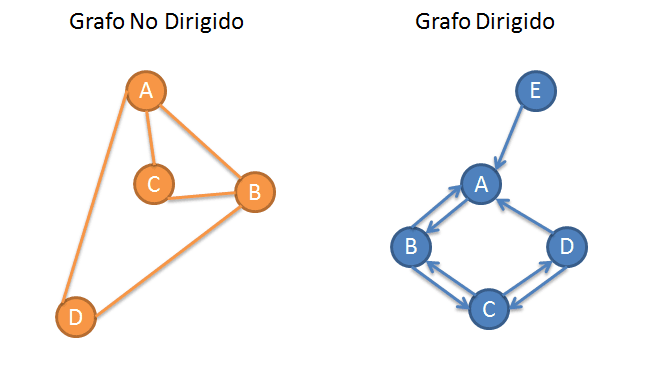
Cuando las aristas conectan los dos puntos de manera simétrica (por ejemplo una correlación, donde A se relaciona con B igual que B con A), decimos que tenemos un grafo no dirigido. Cuando esta conexión no es simétrica, como en nuestro caso tenemos un grafo dirigido (¿se acuerdan que las pendientes de la regresión no son iguales si intercambiamos A y B?). Cuando un oso se come un grafo, tenemos un grafo digerido.

La relación entre todas estas regresiones simples nos permite montar un grafo bastante bastante más accesible de mirar que la tabla anterior.

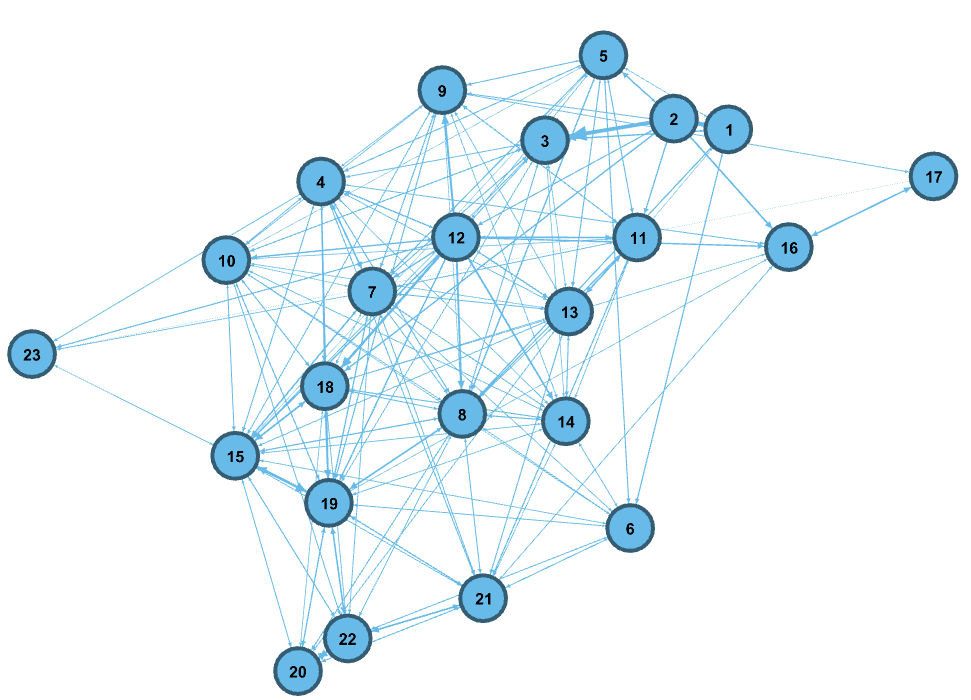
Epa, cómo empiezan a aparecer las relaciones.

Así, podemos empezar a ver cómo se ordenan las preguntas en función de qué tan poderosa es cada una de ellas para predecir los resultados de las demás. Inclusive, uno puede empezar a mirarlas e imaginar agrupamientos funcionales: ¿será que 2, 3 y 5 son tan parecidas entre sí que forman un agrupamiento funcional a tener en cuenta? ¿y 15, 18 y 19?

Esto quiere decir que llegado este punto estaría buenísimo estudiar cómo las preguntas se agrupan de acuerdo al poder predictivo de unas sobre otras, y hacerlo de una manera mejor que ‘a ojo’. Pero, antes de agruparlas, nos toca pensar qué esperaríamos encontrar y ver si los resultados confirman eso o nos sorprenden.

Momento de hipótesis. Por cómo está armado el experimento, esperamos que existan dos efectos de ‘agrupamiento’: el primero tiene que ver con la proximidad de una pregunta a otra y el segundo con su relación temática.

Las preguntas que se siguen una de otra tienen algún poder predictivo entre sí porque cuando uno se distrae lo hace de a ratos. Capaz estabas distraído en las preguntas 5, 6 y 7, pero luego volviste a concentrarte. Si las medidas hubieran sido hechas de forma controlada en un laboratorio, este efecto podría incluso despreciarse pero, dado que los datos son tomados online y de forma no controlada, aquí lo observamos.

Por otro lado, esperamos un efecto de agrupamiento independiente del orden, que tiene que ver con cuán parecidas son las preguntas entre sí: las de rotación espacial deberían agruparse juntas y por separado de las de, por ejemplo, cálculo de sumas y restas. De hecho, al armar el cuestionario, imaginamos 7 grupos:

Comparaciones
Sumas
Restas
Multiplicaciones
Porcentajes
Rotación espacial
Numerosidad (capacidad de decir a golpe de vista cuántas cosas hay en una imagen).

¿Qué fue lo que pasó? Corriendo un algoritmo de aprendizaje automático capaz de agrupar las preguntas entre sí y forzando la aparición de 7 grupos (que es el número de conjuntos de preguntas que estimamos cuando armamos el cuestionario), obtuvimos el siguiente agrupamiento:

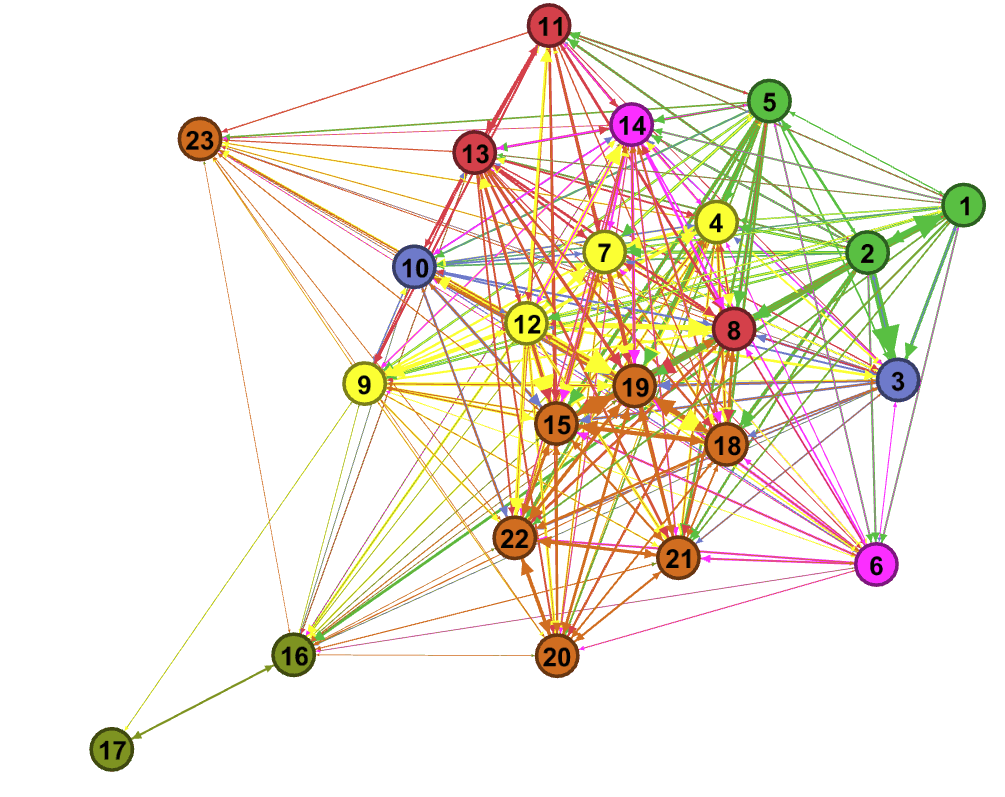
Lo hermoso de ver estos agrupamientos es que el algoritmo no sabe el contenido de las preguntas: solamente sabe cómo se relacionan entre sí a través de las respuestas correctas o incorrectas que dieron los 18K usuarios. La pregunta interesante es si este agrupamiento basado en las respuestas es parecido o distinto (y cómo) del que imaginamos al preparar el cuestionario.

¿Qué tan consistente era nuestra expectativa con lo que al algoritmo agrupó en base a los resultados y sin tener idea del contenido? La respuesta te sorprenderá: MUY.

Bueno. Muy pero no tanto. El algoritmo también encontró grupos consistentes (¡qué bien!) pero no exactamente iguales a los que habiamos imaginado (¡qué mal!, bah, en realidad no fue un qué mal, si no más bien un qué interesante, pero el meme cerraba mejor). A estos grupos, que podés ver separados por colores en el gráfico de arriba, los llamamos así:

Conteo y comparación de dos números simples (verde claro)
Sumas y restas simples (azul)
Multiplicación y sumas y restas compuestas (amarillo)
Comparación de diferencias (violeta)
Lenguaje (rojo)
Porcentaje y rotación espacial (naranja)
Numerosidad (verde oscuro)

Aquí aparecen las primeras cosas interesantes:

La preguntas de porcentaje (15, 18 y 19) se agrupan junto a las de rotación espacial. Esto es muy llamativo. Parece indicar que cuando representamos un porcentaje lo hacemos a través de los sistemas visuales, como si “viéramos” una superficie a la que le sacamos un pedazo y estimáramos el tamaño de ese pedazo en relación al de la superficie. Surge naturalmente una pregunta: ¿cuántos de los sesgos que tenemos a la hora de estimar porcentajes, bien estudiados por Kahneman y sus secuaces de la economía del comportamiento, tienen que ver con esta forma de representar porcentajes?
Inesperadamente, el algoritmo de agrupamiento nos hizo dar cuenta de que las preguntas 6 y 14 son ambas de comparación de diferencias. Estas preguntas están separadas de las de comparación simple.
Observen que los nodos amarillos representan las cuentas más complejas: las de multiplicar o hacer sumas y restas compuestas. Estos cuatro nodos amarillos parecen dividir el grafo en dos. Los grupos que tienen nodos en ambos lados, rodeando a los nodos amarillos, son el de cuentas simples (azul), el de lenguaje (rojo) y el de comparación de diferencias (violeta). Sin rodear los nodos amarillos, pero cerca, están las preguntas de conteo (verde oscuro) y de porcentaje (algunas de las naranjas). Por último, las preguntas de numerosidad (verde oscuro) y de rotación espacial (algunas de la naranjas), son las más alejadas.
La pregunta 23, de numerosidad, no está agrupada tan fuertemente a las otras dos de numerosidad, las 16 y 17 sino que parece más agrupada a las tres preguntas que la precedieron, la 20, 21 y 22. Atribuimos este hecho a que era la última pregunta y muchos participantes ya estaban, hacía un par de preguntas, distraídos y fiacosos.
Este análisis abre muchas preguntas, por ejemplo: acorde con estas relaciones, la probabilidad de hacer correctamente una cuenta compuesta aumenta más si alguien sabe expresarse correctamente que si sabe rotar espacialmente un cuerpo. Existen varias preguntas de este tipo, todas las cuales llevan a una aún más intrigante: ¿se puede inferir la organización lógica o incluso anatómica del cerebro a partir de la aplicación de la teoría de grafos a las respuestas dadas en diferentes test cognitivos?¿Alguien lo hizo antes o estamos descubriendo territorio virgen y fértil de exploración?

Regresiones multiples

Más allá de entender cómo se agrupan los tests, nos interesa responder a otras dos preguntas:

¿Qué tests tienen mayor poder predictivo sobre todos los demás?
¿Qué tests son más fácilmente predecibles a partir del resultado de los demás?

Para responder a estas preguntas corrimos regresiones múltiples en las que, para cada una de las 23 preguntas, incluimos a las otras 22 como variables independientes. Si el agregado de una de estas 22 variables no suma poder predictivo significativo al modelo, esa variable es eliminada. Así, cada una de las 23 preguntas puede tener entre 0 y 22 variables con poder predictivo sobre ella.

¿Qué tests tienen mayor poder predictivo sobre todos los demás?

Para responder a la pregunta de qué test tiene más poder predictivo sobre los demás tests, mostramos un grafo direccionado donde el valor de la conexión entre dos nodos es dado por la pendiente de la regresión en la que el nodo de salida es uno de los regresores incluidos, es decir, es una de las variables independientes. El tamaño del nodo es proporcional a la suma de todas las conexiones salientes del nodo (el Weighted Out Degree), de tal forma que el de mayor tamaño es el de mayor poder predictivo sobre los demás nodos:

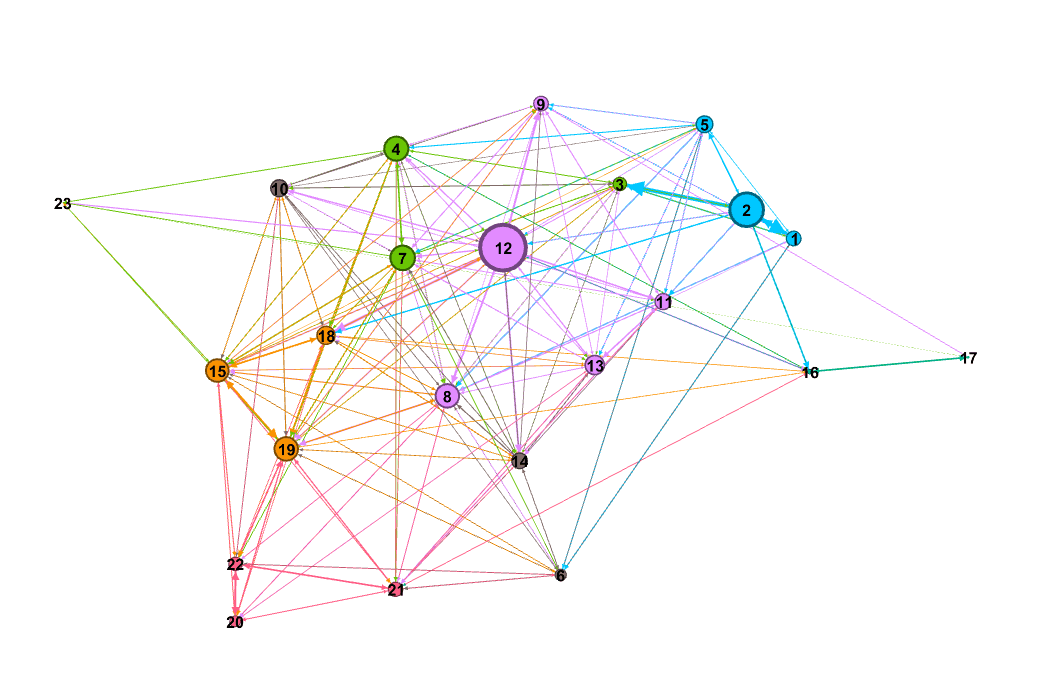
Se ve que el nodo 12 es el de mayor poder predictivo (Un teatro tiene 6 secciones. Cada sección tiene 8 filas y cada fila tiene 10 asientos. ¿Cuántos asientos hay en total?). Esto es razonable ya que esta pregunta no sólo implicaba una doble multiplicación (6x8x10) sino que, además, contiene elementos de imaginería visual y numerosidad.

¿Qué tests tienen mayor poder predictivo sobre todos los demás?

Para responder a la pregunta de cuál de los tests es más fácilmente predecible a partir de los demás (ojo acá con la palabra “predecible”, no queremos decir cuál correlaciona más con otros sino en cuál test la incertidumbre disminuye más a partir del conocimiento del resultado de los demás), hicimos otro grafo direccionado en el que el valor de cada conexión es dado por el valor de la pendiente usando el nodo de entrada como variable dependiente.

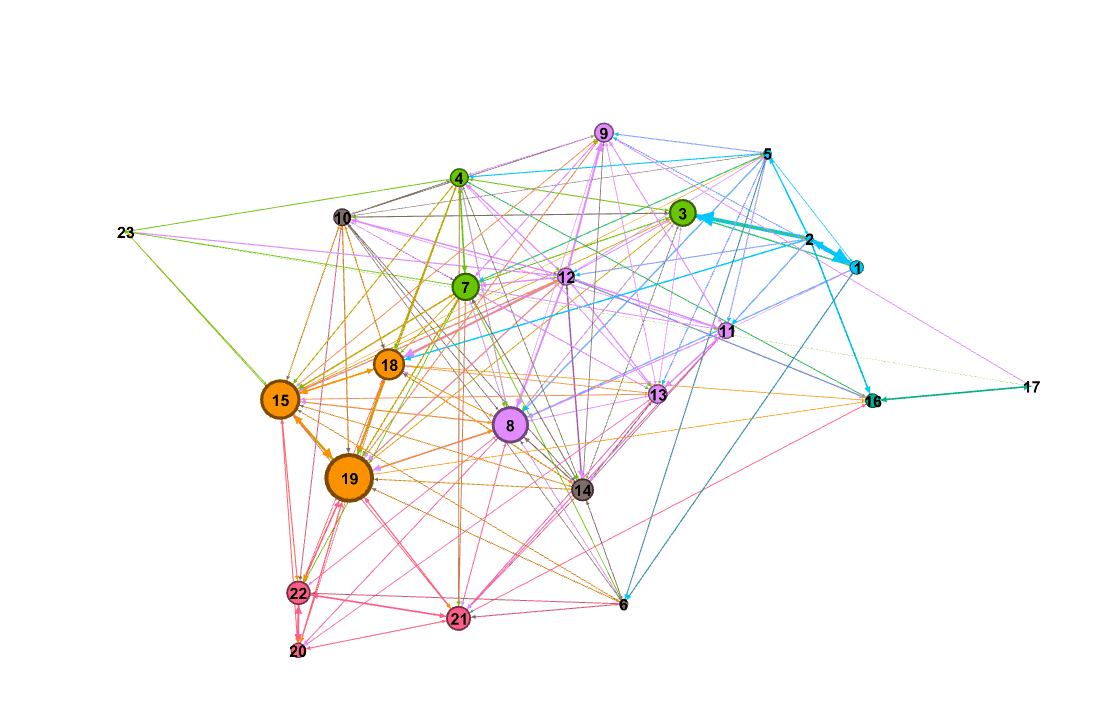
Vemos que las 3 preguntas de porcentaje (15,18, 19) son algunas de las más ‘predecibles’ (y también algunas de las que tienen mayor poder predictivo unas sobre otras). O sea, si alguien hizo bien la 18, la probabilidad de haber hecho bien la 19 aumenta mucho en relación a si no hizo bien la 18.

Todo esto significa que si tuviéramos que elegir conocer el resultado de una pregunta para saber qué tal le fue a alguien en cualquier otra, eligiríamos la 12, que es la que más fuertemente predice sobre las demás. De la misma manera, si nos desafiaran a predecir cómo le fue a alguien en alguna pregunta, eligiríamos responder sobre la 19, que es la más ‘predecible’ teniendo información sobre las demás.

Lo que se viene

Cuando lanzamos “Queso” lo hicimos como prueba de concepto (y MVP) de un experimento bastante más ambicioso en el que queremos entender cómo ayudar a personas adultas con muchas dificultades en aritmética.

La idea era que, por medio de estas 23 preguntas, íbamos a poder identificar a los “quesos” y diseñar juegos o actividades pensando en implementar diferentes estrategias para lograr un aprendizaje significativo.

En ese sentido, el hecho de que ya hayan participado más de 15 mil personas hizo que tuviesemos queso para tirar al techo. Estamos armando diferentes intervenciones que creemos, basados en nuestra experiencia, lecturas y estudios, que pueden ayudar a estas personas a dar un vuelto sin hacerse lio o a jugar con números sin tenerles miedo. Si tenés ideas, son totalmente bienvenidas y te pedimos que nos contactes. Sobre todo si sos docente con experiencia en la enseñanza de aritmética básica.

Otra cosa que descubrimos durante el desarrollo de este experimento (particularmente durante el análisis de datos) es la potencia que tiene elegir formas de expresar visualmente la información de manera que se haga más accesible. Mirar la tabla con la relación entre preguntas era áspero, pero mirar el grafo nos permitió conversar y exprimir el hecho de que somos un grupo super heterogéneo, de manera que los que venían de palos más alejados al análisis de datos pudieran encontrarse con una forma más amigable de acceso a esas grandes cantidades de información. Así, convertimos algo que podían leer un par en algo que podíamos charlar en la mesa. Punto para el diseño y para la interdisciplina.

Por último, pasó algo que no esperábamos. Dado todo lo que discutimos, se nos abrió un nuevo proyecto megalómano, basado en la pregunta que nos hicimos más arriba y que repetimos acá: ¿se puede inferir la organización lógica o incluso anatómica del cerebro a partir de la aplicación de la teoría de grafos en la estructura de relación de las respuestas dadas en diferentes test cognitivos?

No sabemos. Pero sí sabemos que nadie lo intentó y que nos encanta la idea de hacerlo, así que decidimos que vamos a lanzar un nuevo test, no con 23 preguntas, sino con 100 (o algo así, muchas más que 23). Y esas 100 (o por ahí) no van a ser sólo sobre matemática sino también sobre lenguaje, memoria, razonamiento abstracto, inhibición de impulso y otras habilidad cognitivas. Si estás leyendo esto y tenés buenas ideas sobre posibles tests para incluir porque querés entender cómo se relacionan esos tests con todos los demás que vamos a hacer, somos todos oídos. Nos encantaría escucharte y que seas parte de esta idea megalómana.

¡Ah! El spoiler alert: para evitar correlaciones espurias entre preguntas consecutivas, en la nueva versión del test (que ya está online) las 23 preguntas aparecen en orden aleatorio. La idea es sacarnos de encima el factor de proximidad.

Como siempre, lo que aprendamos (y las preguntas que nos hagamos), las vamos a ir compartiendo por acá. Nos queda agradecer el amor y el aguante.

Compartir realmente es bancar. Estamos pudiendo hacer cosas que no nos imaginamos posibles gracias a la participación de tantos, tantos de ustedes.

TXTLabs