Hace un tiempo lanzamos un experimento relacionado a un proyecto al que llamamos Queso. Hoy, ese proyecto se llama Cognitoma, no sólo porque es mucho más adecuado y ―¿por qué negarlo?― un poco más lindo, sino por una razón más importante que les vamos a contar más adelante. Wait for it.
En ese experimento, más de 22 mil participantes respondieron 23 preguntas relacionadas a habilidades matemáticas. Tardaron un promedio de aproximadamente 7 minutos cada uno, lo que quiere decir que teníamos más de 2.200 horas de esfuerzo mental en nuestras manos (y nuestros servidores).
Un análisis preliminar de esos datos arrojó una hipótesis jugada y curiosa: para hacer estimaciones de fracciones o porcentajes, usamos circuitos mentales asociados a la memoria visuo-espacial y la rotación mental. Hipótesis que no debería resultarles una novedad si ya leyeron la precuela de este artículo, acá. En síntesis, es como si, a la hora de estimar un porcentaje, imaginásemos un espacio al que “le sacamos un cacho” y estimáramos el tamaño del cacho en relación al del espacio imaginado.
Aunque las sospechas se hacían evidentes cuando analizábamos cómo cambiaba la probabilidad de haber hecho bien una pregunta si habías hecho bien alguna otra o no, es decir, cuando analizábamos el poder predictivo de unas habilidades sobre otras, todavía nos faltaba analizar cómo las diferentes habilidades cambiaban en promedio según la edad, el nivel educativo y el género de cada persona. La idea subyacente era ver si, también en función de estas variables, podíamos hallar una similitud entre habilidades espaciales y de estimación de porcentajes. En términos más técnicos, nos faltaba hacer un análisis de regresiones con los datos demográficos.
En esta segunda entrega les contamos cómo hicimos lo que hicimos y les adelantamos un final feliz: el nuevo análisis ―el de las regresiones― lanzó un resultado confirmatorio de nuestra hipótesis. Con esta historia escribimos un paper que acabamos de enviar a una revista científica y que ahora mismo está en proceso de revisión.
Así que, como queremos seguir cumpliendo a puro empuje y ganas el compromiso de compartir cada paso de una investigación, aquí estamos. En el proceso de ir desde la idea a la implementación, los debates, el envío a la revista, los revisores y, si tenemos suerte, tal vez, la publicación, lo que ahora van a leer es una mezcla entre la traducción del paper que acabamos de enviar (de hecho, van a ver que las figuras están en inglés, ya que son las mismas del paper) y un artículo de comunicación de ciencia. Y, aunque en la primera entrega ya compartimos algunas ideas preliminares y esta es una secuela, decidimos escribirla de manera tal que se entienda sin haber leído el artículo anterior.
Arranquemos.
Algunos conceptos para empezar
La estimación automática y perceptual del número de elementos en un conjunto, es decir, el hecho de que sin contar podamos saber si en una mesa hay uno, dos, tres, cuatro o más platos, se implementa en el cerebro a través de un sistema neuronal denominado Sistema Numérico Aproximado. Esta habilidad, evolutivamente heredada y presente transversalmente en diferentes especies, de monos a abejas, se conoce comúnmente como numerosidad y muchos investigadores argumentan que el concepto abstracto de número natural se apoya en ella. [Butterworth, 2005; Dehaene, 2004; Dehaene, 2011; Feigenson, 2004; Xu, 2005].
Distintos estudios actuales intentan expandir el alcance de este modelo. Por ejemplo, investigaciones recientes sugieren que también tenemos la capacidad de estimar de forma perceptual, automática y holística el valor de una fracción [Butterworth, 2005; Dehaene, 2004; Dehaene, 2011; Feigenson, 2004; Xu, 2005]. Esto vendría a significar que, si te muestro la fracción 7/23, antes de que hagas la cuenta y sepas que da aproximadamente 0,3, tu cerebro ya lo estimó y puede usar esa estimación inconsciente a la hora de guiar tu comportamiento. Así, existen dos formas que nuestro cerebro usa para estimar una fracción: si hace falta, y sabe cómo, hace la cuenta exacta; si no, de todas formas, ya tiene computada una estimación [Jacob, 2012]. A esta teoría de cómo se procesan y representan las fracciones en el cerebro la llamamos Teoría de la Doble Representación de Fracciones.
¿Cuáles fueron nuestros objetivos?
Lo que propusimos en este trabajo (a partir de la evidencia que obtuvimos gracias a ustedes, que participaron en el experimento) es que estas dos habilidades −la numerosidad y la estimación de fracciones− son distinguibles y disociadas, aunque pertenezcan a un grupo de habilidades matemáticas interrelacionadas. El objetivo de la investigación fue explorar cómo estas dos habilidades se relacionan entre sí y, también, al conjunto más amplio de habilidades matemáticas, a través del estudio de los patrones de respuestas a diferentes problemas matemáticos en un gran número de personas (22.221 para ser más precisos, un montón).
¿Qué esperábamos?
Basados en investigaciones previas, esperábamos dos cosas: (1) que la estimación perceptual de fracciones o números enteros mostraran diferentes patrones de relación con otras habilidades y (2) que estos patrones revelaran que la estimación de fracciones se hace tanto de forma automática y perceptual, con patrones similares a los de otras percepciones, como a través de un cálculo exacto, cuando se sabe cómo; es decir, estos patrones darían sustento a la Teoría de la Doble Representación de Fracciones.
¿Cómo hicimos el experimento?
Para poder realizar este estudio, desarrollamos una plataforma online y adaptamos tests estandarizados para la evaluación del desempeño en matemática e, incluso, utilizados para detectar trastornos del aprendizaje [Aster, 2000; Elliot, 1997; Jastak, 1993; Jordan, 2007; Kosc, 1974; Landerl, 2004; Moyer, 1967; Shalev, 2005; Wechsler, 1997]. Como pudieron apreciar si participaron del experimento (y si no lo hicieron, van a tener revancha dentro de poco), la interfaz estaba diseñada para ser amigable y todo el asunto podía resolverse en pocos minutos. Esto nos permitió algo muy importante: tomar una gran cantidad de datos. ¿Y por qué está buenísimo tener muchos datos? Porque podemos medir pequeños efectos sin que queden escondidos en el ruido propio de una muestra con muchos menos participantes.
La tarea consistía en responder 23 problemas presentados en orden creciente de dificultad para tratar de que te enganches y termines. Una parte de los participantes respondió a las preguntas en orden aleatorio (sin saberlo), para controlar que los efectos observados no fueran debidos al orden en que se presentaron los problemas.
Las 23 preguntas evaluaban estimación de fracciones (en forma de porcentajes), numerosidad, conteo, comparación de números, sumas, restas y multiplicaciones simples, memoria visuo-espacial y el entendimiento de problemas aritméticos contextualizados [Hartshorne 2015].
¿Cómo analizamos los datos?
Para analizar los patrones de relación entre las diferentes habilidades matemáticas, hicimos dos análisis: regresiones y análisis de grupo. Las regresiones nos permiten entender en qué medida el desempeño en una habilidad en función de la edad, el nivel educativo, el sexo u otra variable cuya influencia queramos analizar, se parece con el desempeño en otra habilidad cualquiera en función de esas mismas variables. En otras palabras, nos permite cuantificar cuán parecidos son, para dos habilidades diferentes, los gráficos de desempeño vs. edad (o vs. nivel educativo, por ejemplo). El análisis de grupo nos permite agrupar las habilidades a partir de sus similitudes, partiendo de la idea de que dos ideas son similares si el buen desempeño en una de ellas es un buen predictor de buen desempeño en la otra.
¿Qué encontramos?
El análisis de grupo mostró una gran similitud entre estimación de fracciones y memoria visuo-espacial, pero no entre estimación de fracciones y numerosidad. Es decir que el hecho de que una persona sea mejor que el promedio estimando, por ejemplo, a qué porcentaje de 30 equivale 6, nos dice que es probable que también sea mejor encajando piezas en el espacio pero no que sea mejor estimando cuántos platos hay en una mesa con muchos platos. Las regresiones mostraron de forma independiente evidencia convergente hacia la misma idea: la de una relación robusta entre estimación de fracciones y la memoria visuo-espacial [Jacob, 2012]. Adicionalmente, las regresiones mostraron evidencia favoreciendo la teoría de la doble representación de fracciones en el cerebro (que, recordemos, era la teoría que dice que a las fracciones las estimamos perceptualmente además de poder calcularlas). Las regresiones mostraron que la capacidad de estimar fracciones se comporta en relación a la edad y al género de una persona como se comporta la capacidad de memoria visuo espacial, lo que sugiere una dinámica propia de la percepción, y que, además, la capacidad de estimar fracciones aumenta con la educación como aumenta la capacidad de cálculo, lo que sugiere un componente no perceptual.
¿Qué concluimos?
Tanto el análisis de grupos como las regresiones sugieren un fuerte solapamiento entre los circuitos cerebrales para la memoria visuo-espacial y para la estimación de porcentajes. En contraste, la numerosidad parece estar disociada. Es, incluso, la única habilidad matemática cuyo desempeño no mejora con el nivel educativo. También es, de las que medimos, la única en donde las mujeres mostraron un mayor desempeño que los varones.
En criollo: cuando tenemos que estimar una fracción y no podemos o no queremos hacer el cálculo, usamos circuitos cerebrales de representación del espacio, como si imagináramos un pedazo de espacio, le sacáramos un cacho y tratáramos de estimar cuánto es el cacho en relación al pedazo.
¿Cómo podría seguir esta investigación?
Queda por entender si este mecanismo perceptual puede colaborar en el aprendizaje del concepto abstracto de fracción. Trabajar a través de un conjunto de ejemplos perceptuales amplios y variados tal vez ayude a consolidar las intuiciones necesarias para la comprensión del concepto de fracción, más allá del aprendizaje de los algoritmos necesarios para hacer el cálculo exacto. O incluso como forma de mejorar o acelerar el aprendizaje de estos algoritmos.
¿Y el cambio de nombre?
¡Ah! Eso.
El nombre “Queso” daba a entender que el experimento estaba relacionado con la búsqueda de personas que fueran malas para las matemáticas (“quesos”). Si bien este fue un primer objetivo del proyecto, al recabar tanta cantidad de datos y empezar a encontrar relaciones jugosas, aumentó nuestra ambición científica en estos resultados. Pensamos, entonces, que podríamos encontrar vínculos entre variables y analizar factores como nivel educativo, edad y género (lo que, justamente, estudiamos en este trabajo). Pero la literatura científica nos esperaba con una advertencia: las mujeres suelen tener peores resultados a la hora de resolver tests cuando, previamente, se les hace hincapié en ciertos estereotipos que sugieren que “los varones son mejores” en ciertas habilidades, por ejemplo, las matemáticas. Y NUESTRO EXPERIMENTO SE LLAMABA QUESO.
Sí, era posible que el nombre no influyera en los resultados. Pero no lo sabíamos y queríamos asegurarnos. Decidimos, entonces, renombrar el proyecto como “Cognitoma”, modificar el texto que daba la “bienvenida” al experimento, lanzarlo nuevamente para tener una “tanda” de participantes libres del prejuicio gruyere y analizar si los resultados seguían manteniendo su correlación.
Y así fue.
Ahora la cuestión se va a poner un poquito más técnica (anímense, no se van a arrepentir).
Resultados generales y performance
En promedio, los participantes tardaron casi 7 minutos (400 segundos) en responder las 23 preguntas (Figura 1a) y la performance disminuyó a medida que el test progresaba (Figura 1c). La edad pico de performance fue de 35 años (más de lo que esperábamos, hay esperanzas) (Figura 1d). Los resultados también mostraron que aquellos a los que les fue mejor sufren un menor impacto de la edad sobre la velocidad a la que hacen el test (Figura 1b). Esto es consistente con un estudio publicado recientemente donde más de 6 mil personas fueron estudiadas durante 29 años, mostrando que entre más de 65 factores de riesgo, la mortalidad está fuertemente asociada al deterioro cognitivo y la disminución en la velocidad de procesamiento [Aichele, 2015].
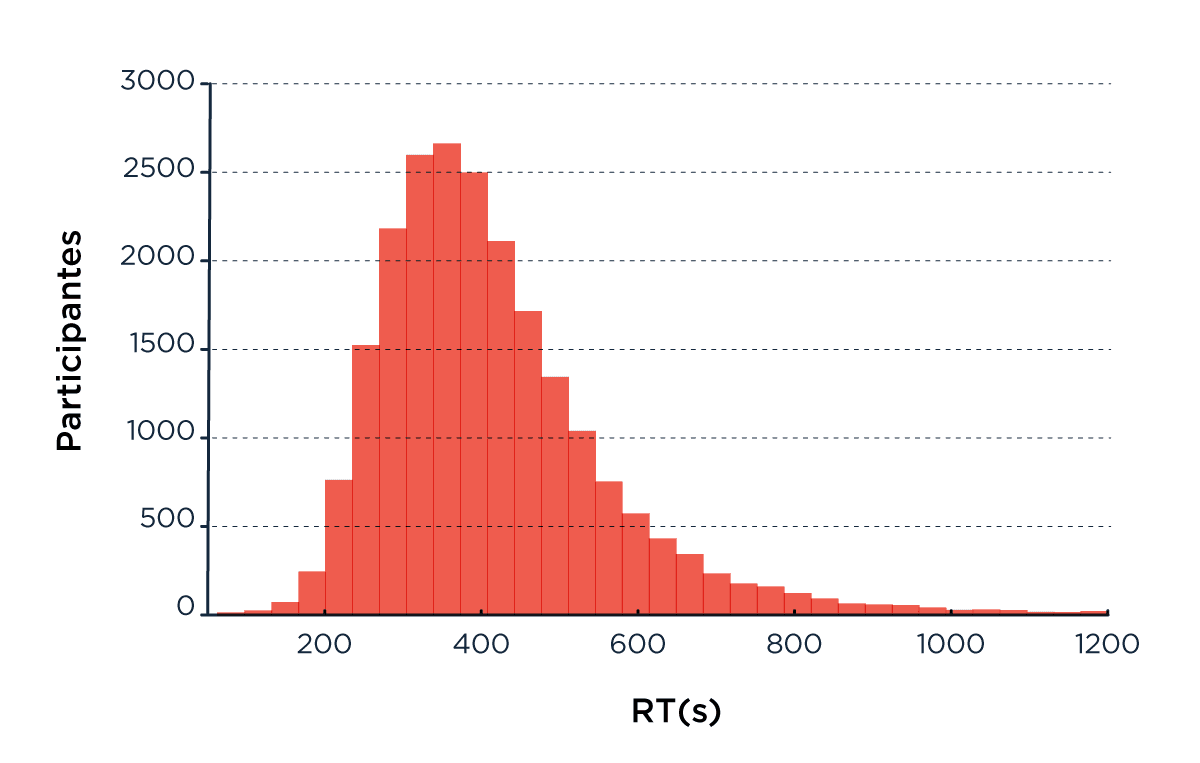
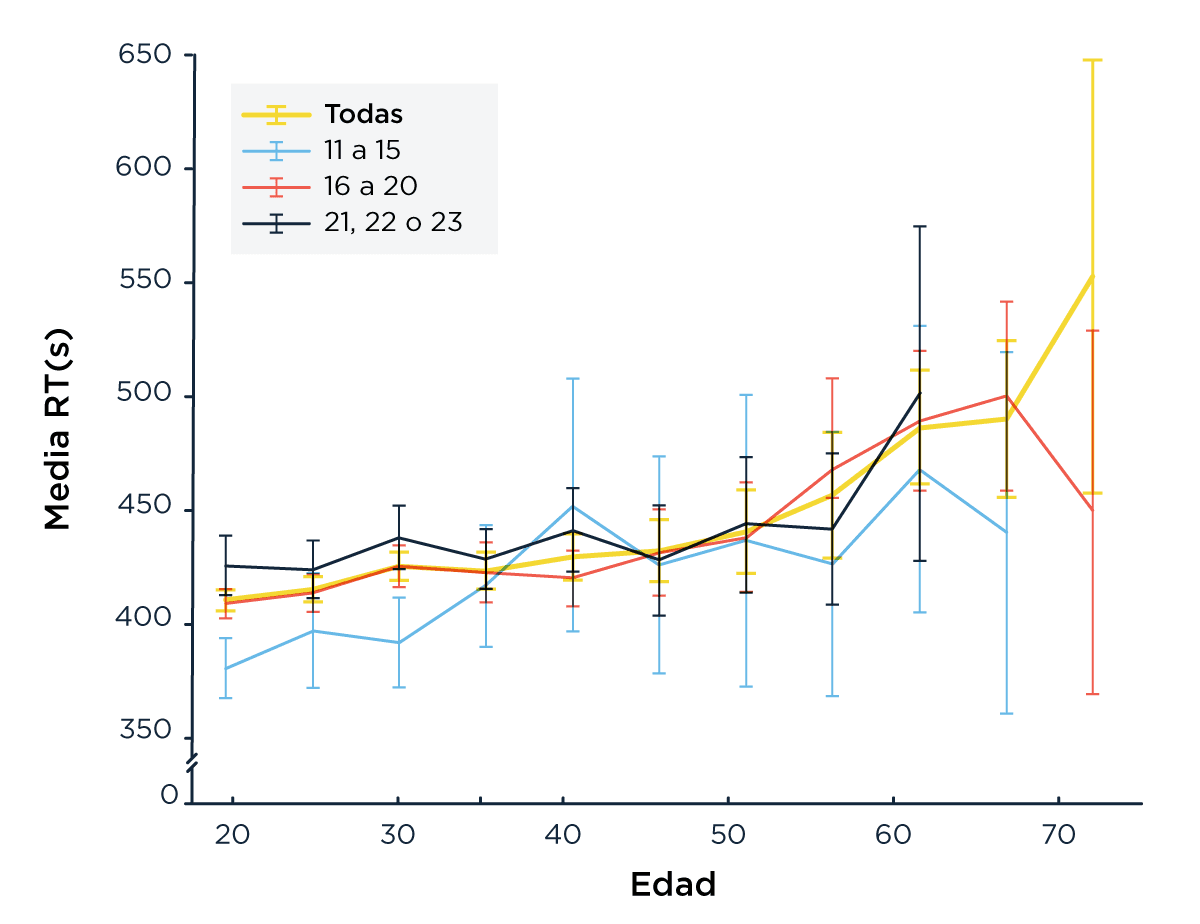
Figura 1: (a) Tiempos de respuestas para los 23 ítems. (b) tiempo promedio por edad y número de aciertos (las barras de error muestran el error estándar); las tres curvas son par participantes que aciertan de 11 a 14, de 16 a 20 o,de 21 a 23 ítems.
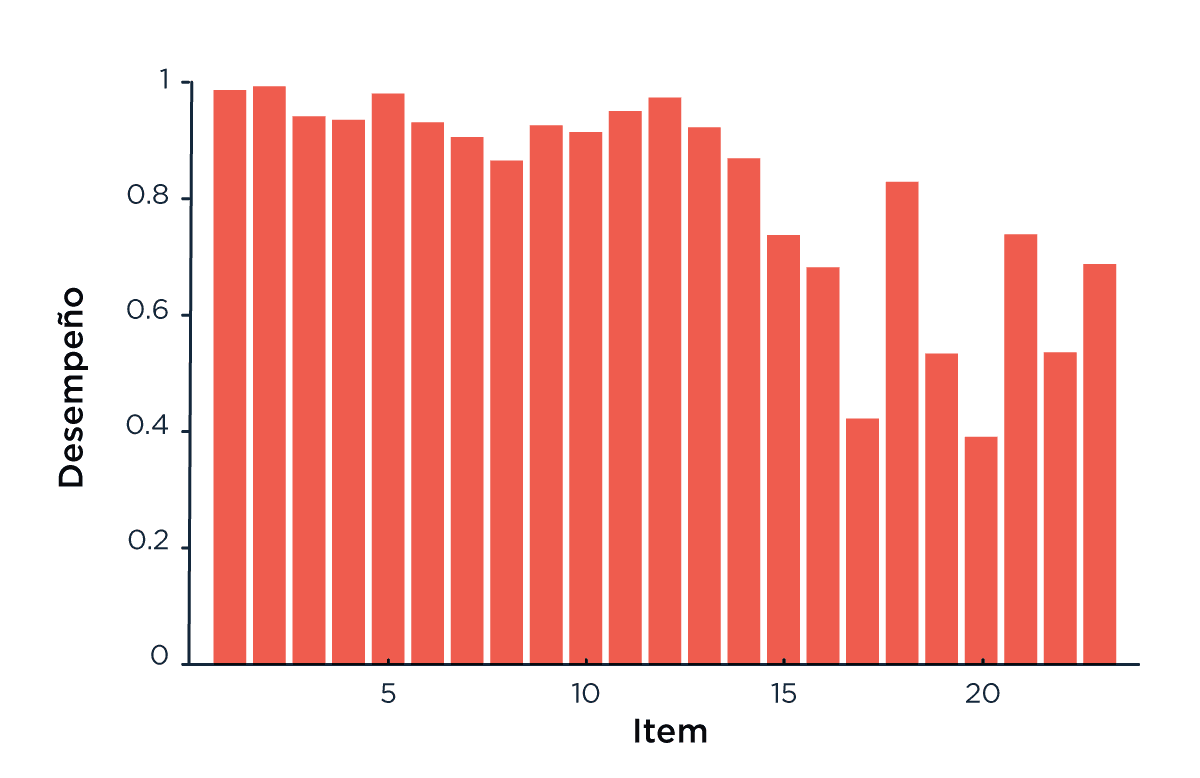
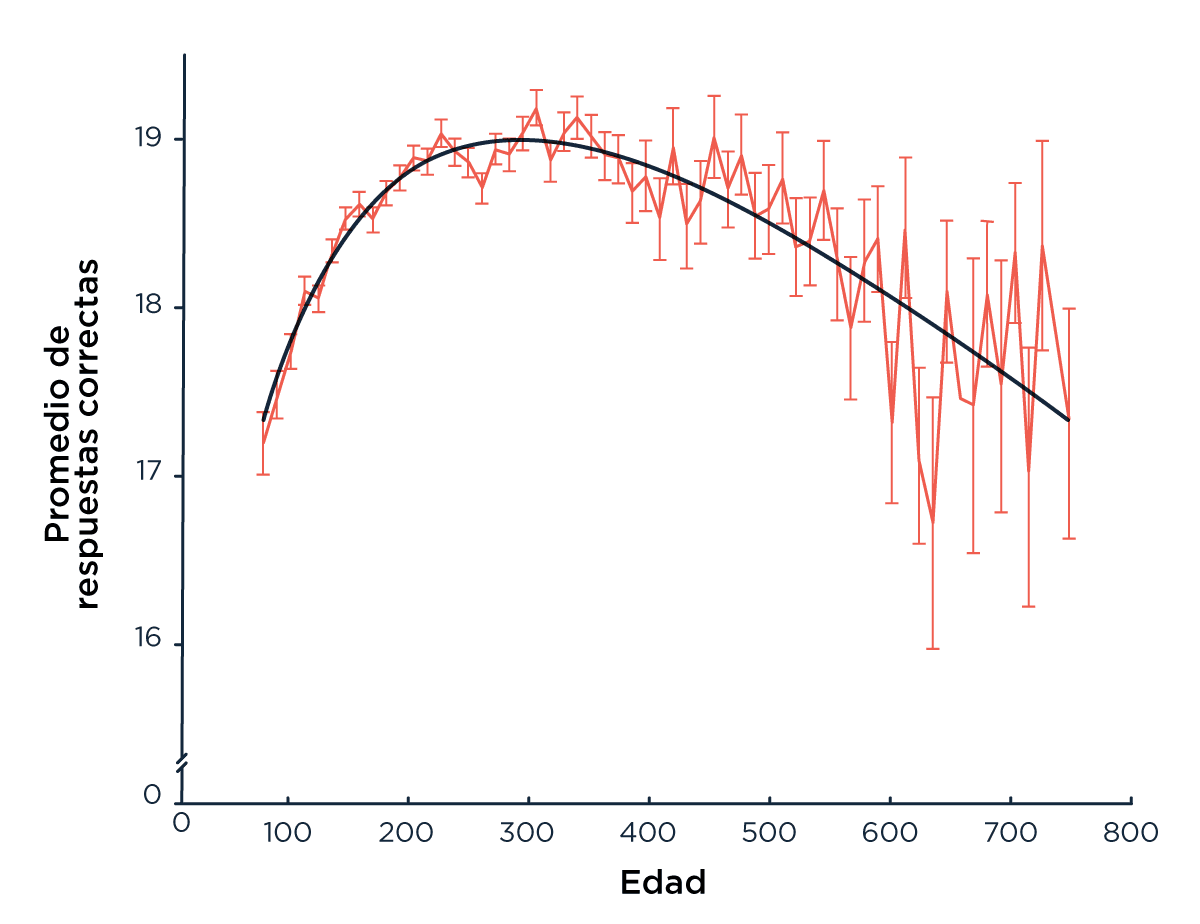
Figura 1: (c) Porcentaje de aciertos para cada ítem (d) Número promedio de aciertos por edad (las barras de error muestran el desvío estándar), y ajuste parabólico con la edad en escala logarítmica.
Análisis de grupo
Lo primero que hicimos fue calcular para cada par de preguntas cómo la probabilidad de haber contestado bien una cambiaba de acuerdo a si el participante había hecho bien o no la otra. Dicho más técnicamente, calculamos la pendiente de la regresión simple usando como variable binaria independiente la respuesta a una de las preguntas y como variable binaria dependiente la respuesta a la otra.
Ese valor, el de la pendiente de la regresión entre cada par de preguntas, fue utilizado como arista en un grafo donde cada nodo era una de las 23 preguntas (Figura 2b). Usamos este grafo para analizar la similitud entre preguntas, dado el valor de la arista que conecta los dos nodos, y agruparlas.
Pero… ¿cómo agruparlas?
En primer lugar, sabíamos que la similitud entre dos preguntas aumenta si aumenta el valor de la arista que las une, ya que el haber hecho bien una pregunta hace que cambie más la probabilidad de haber hecho bien también la otra: son preguntas que exigen habilidades similares. Además, necesitábamos algún parámetro que pudiéramos establecer como criterio para decir que, si dos preguntas son más similares que el valor del parámetro, entonces pertenecen a un mismo grupo, y si no, no. Si este parámetro tuviera un valor muy bajo, entonces todas las preguntas pertenecerían a un solo enorme grupo porque bastaría con que dos preguntas sean apenas similares para que se las considere parte de un mismo grupo. Por el contrario, si ese parámetro tuviera un valor muy alto, cada pregunta quedaría aislada y no se formaría ningún grupo porque el criterio sería tan riguroso que sólo dos preguntas muy muy similares podrían agruparse. Y esto no era todo. La situación era más complicada: dos preguntas podrían no tener valor predictivo una sobre la otra (la arista que las une tendría en este caso valor cero), pero sí las dos sobre una tercera. O la tercera podría tener valor predictivo sobre esas dos, lo que no es lo mismo… ¿Qué hacemos en ese caso?
Por suerte la ciencia es un emprendimiento colectivo: un montón de gente antes de nosotros se encontró con este problema de agrupar cosas según su similitud e inventó formas de hacerlo. Una de las más famosas y populares es el método de Ward, creado por, claro, Joe H. Ward [Ward, 1963; Gama, 2018]. El método incluye la definición del parámetro que mide similitud entre dos nodos. Cómo varían los grupos de acuerdo al valor de ese parámetro se suele representar con algo que se llama dendograma (Figura 2a). Para un valor de similitud como el mostrado en la línea horizontal en la Figura 1a, es decir 0,97, obtenemos un agrupamiento de acuerdo al mostrado por los colores en el grafo de la Figura 2b. La disposición de los nodos en el grafo se establece según un algoritmo que simula algo así como una repulsión electroestática en 2D entre los nodos.
Acá aparece la primera evidencia fuerte de la robusta asociación entre memoria visuo-espacial y estimación de fracciones: el algoritmo las agrupó, las puso en el mismo grupo. Esto en sí fue una sorpresa. Pensábamos que la estimación de fracciones debía estar más asociada a la capacidad de hacer cuentas simple, o comprender problemas aritméticos contextualizados, por ejemplo. Pero no. Bella ciencia.
Los grupos que se formaron y la denominación que les dimos fueron los siguientes: fractions magnitude estimation en rojo (ítems 15, 18, and 19), visuo-spatial working memory en azul (ítems 21, 22, and 23), memory recall for simple arithmetic problems (items 1 and 2) en amarillo, sums and subtractions (ítems 3, 4, and 5) en verde, comparison of differences (items 6 and 14) también en amarillo, complex sums and multiplications (ítems 7, 8, 9, 10, 11, 12, and 13) también en azul, numerosity (16, 17) también en rojo, y spatial numerosity (23) en verde.
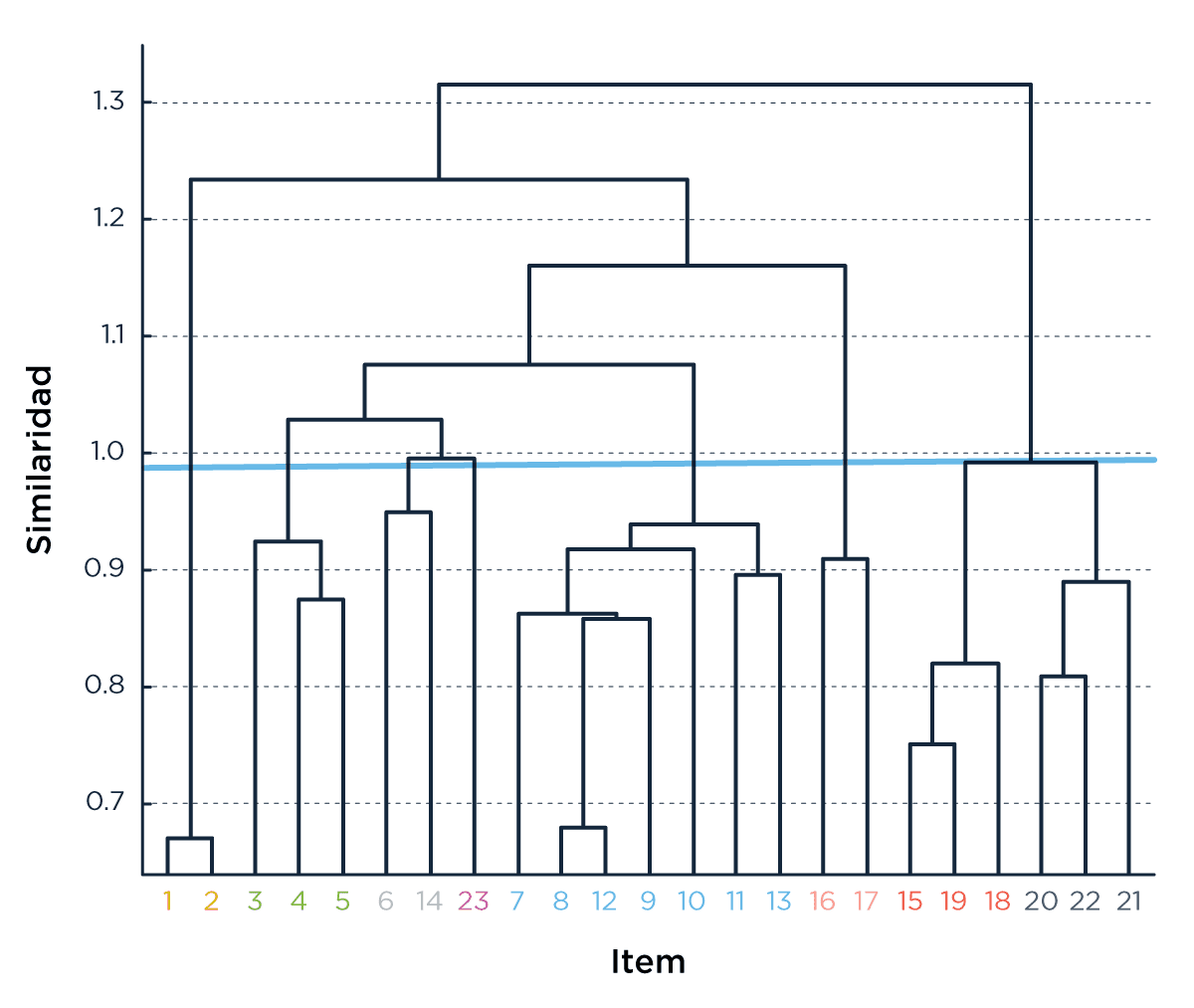
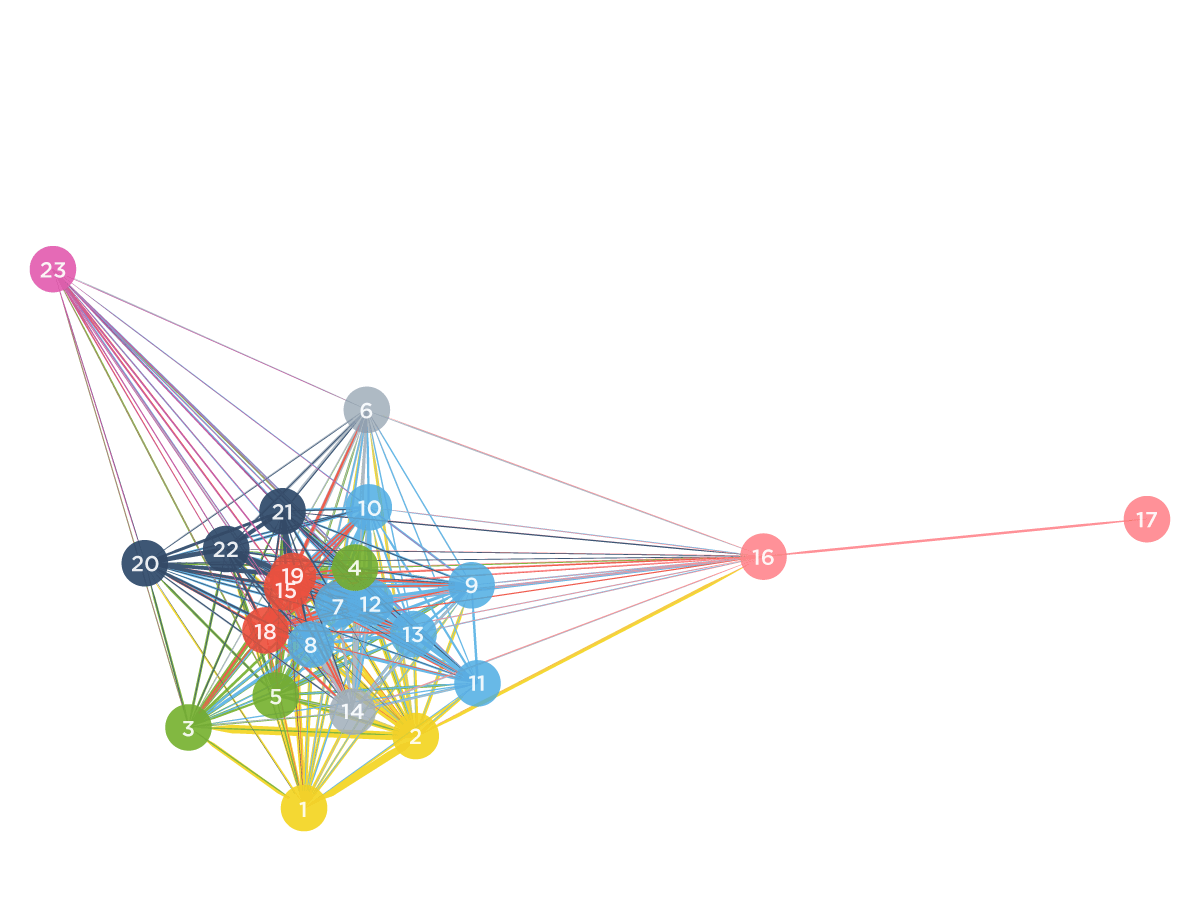
Figura 2: (a) Dendrograma. (b) grafo de ítems. El color de los nodos es dado por el agrupamiento para un nivel de similaridad de 0,97 (la línea horizontal en (a). La posición de los nodos se obtiene a partir de una proyección multidimensional en el plano [Kruskal, 1978].
El agrupamiento de los ítems 15, 18 y 19, de estimación de fracciones, junto a los ítems 20, 21 y 22, de memoria visuo-espacial, así como el agrupamiento de los ítems 16 y 17 (numerosidad) y de los ítems 1 y 2 (memoria) son muy robustos: no cambian si usamos otros métodos en lugar del Ward o si usamos en vez de la pendiente de las regresiones, por ejemplo, las correlaciones entre dos ítems. Cómo se agrupaban los otros ítems (de 3 a 14) es más sensible al método usado, pero esos cambios no modifican la interpretación de los resultados que hacemos a continuación.
Análisis de las regresiones
Analizamos la performance en los diferentes grupos de preguntas de acuerdo a la edad, el nivel educativo y el género, variables que, se sabe, suelen tener valor predictivo en los tests cognitivos. La idea era obtener evidencia convergente para el agrupamiento logrado arriba. Si, por ejemplo, la estimación de fracciones depende de circuitos mentales solapados con los de memoria visuo-espacial, entonces estas habilidades deben demostrar dependencias con la edad, la educación y el género similares. A su vez, las regresiones pueden brindar, como veremos más adelante, evidencia en favor de la hipótesis de la doble representación de las fracciones.
En vez de analizar directamente la performance, es decir, el porcentaje de preguntas que un participante hizo bien o mal, analizamos cuánto mejor es una persona en relación al desempeño promedio, y lo usamos tomando como medida la dispersión promedio. Por ejemplo, en vez de decir “Fulana hizo 0.9 de las preguntas bien, o sea, su desempeño fue de 0.9”, decimos “el desempeño de Fulana estuvo dos desvíos estándares por encima del promedio de la población”. Esta variable, que llamamos el z-score, es una medida de desempeño más interesante de usar que el desempeño en sí mismo.
Antes de realizar un análisis más general sobre cómo las tres variables (edad, educación y género) impactan sobre el desempeño en diferentes habilidades (o sea, antes de realizar una regresión multivariada), estudiamos cómo lo hace cada una por separado (es decir, hacemos regresiones simples) para entender la mejor forma de incluirlas en un modelo más general.
Nivel educativo
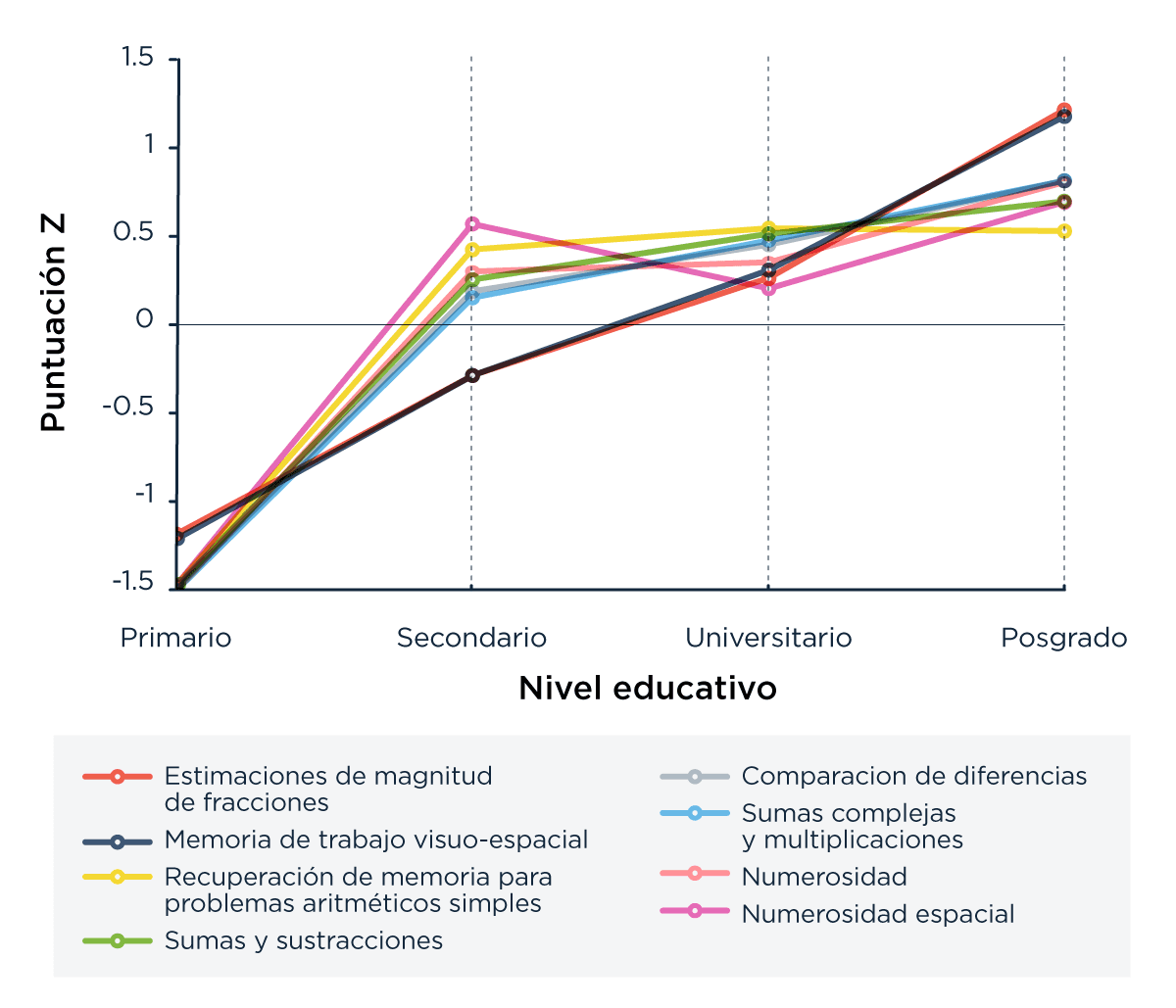
La comparación del desempeño para diferentes habilidades (es decir, grupos de pregunta), medido en términos de z-score, sugiere fuertemente que el desempeño matemático mejora con la educación (Figura 3). Bastante esperable esta no-noticia.
Pero ―atención― primera curiosidad: en el caso de las habilidades de numerosidad y de numerosidad espacial, sin embargo, no vemos un aumento estadísticamente significativo en relación a una mejor educación. Todas las otras habilidades mostraron un incremento significativo.
La segunda curiosidad, relevante para la idea que proponemos, es que las curvas para las habilidades de estimación de fracciones y de memoria visuo-espacial son las más cercanas entre sí: la distancia promedio entre sus puntos es de 0.02 z-scores, por lo menos 10 veces menor que la distancia promedio entre cualquier otro par de curvas de la figura. A pesar de que este hecho parece dar sustento a la hipótesis de que estas dos habilidades están más solapadas, más adelante vamos a mostrar que, en realidad, como la estimación de fracciones depende de la educación, es más parecido a lo que ocurre con los cálculos complejos que a la memoria visuo-espacial. La ilusión que vemos en la Figura 3 es porque no controlamos por edad, es decir, no nos fijamos qué pasa dentro de un mismo rango de edad. Cuando se hace este control vemos que, para una determinada edad, la dependencia con el nivel educativo a la hora de hacer estimación de fracciones se parece más a la observada en cálculos complejos que en memoria visuo-espacial. Volveremos sobre este punto más adelante.
Envejecimiento
Como ya dijimos, la edad pico de desempeño para las 23 preguntas fue de 35 años (error estándar de 0.5 años). También obtuvimos la edad pico de performance para cada uno de los grupos de pregunta (Tabla 1 de este apartado), obteniendo resultados similares a otros previamente publicados en otros estudios [Halberda, 2012], [Lee et al., 2008]. Esto le da validez al método de pedirle a un montón de personas que hagan el experimento y nos ayuden a masificar: los resultados tomados así, vía web, son comparables a los obtenidos con métodos tradicionales presenciales, donde de pueden controlar mejor las condiciones pero se logran muchos menos participantes.
Calculamos la distancia media entre cada curva de desempeño vs. edad (Figura 4) y, otra vez, encontramos que la curva más cercana a la de memoria visuo espacial es la de estimación de fracciones. La distancia promedio entre estas dos curvas es de 0.27 z-scores, mientras que la próxima curva más cercana a la de memoria visuo-espacial es la curva para sumas complejas a una distancia promedio de 0.36 z-scores.
De la figura 4 surge que, en este caso, mejor que suponer una relación lineal es asumir una curva cóncava (más específicamente, una parábola) con la edad en escala logarítmica (la parte de “adelante” de la parábola tiene un incremento mucho más marcado que el decremento de la parte de “atrás”, y modelar el envejecimiento cognitivo de esta forma es práctica común en la escasa literatura que encontramos sobre el tema). Esto es importante porque, cuando intentemos separar los efectos de la edad, la educación y el género en el modelo, nos convendrá asumir esta dependencia parabólica del z-score con la edad para mejorar el ajuste del mismo a los datos.
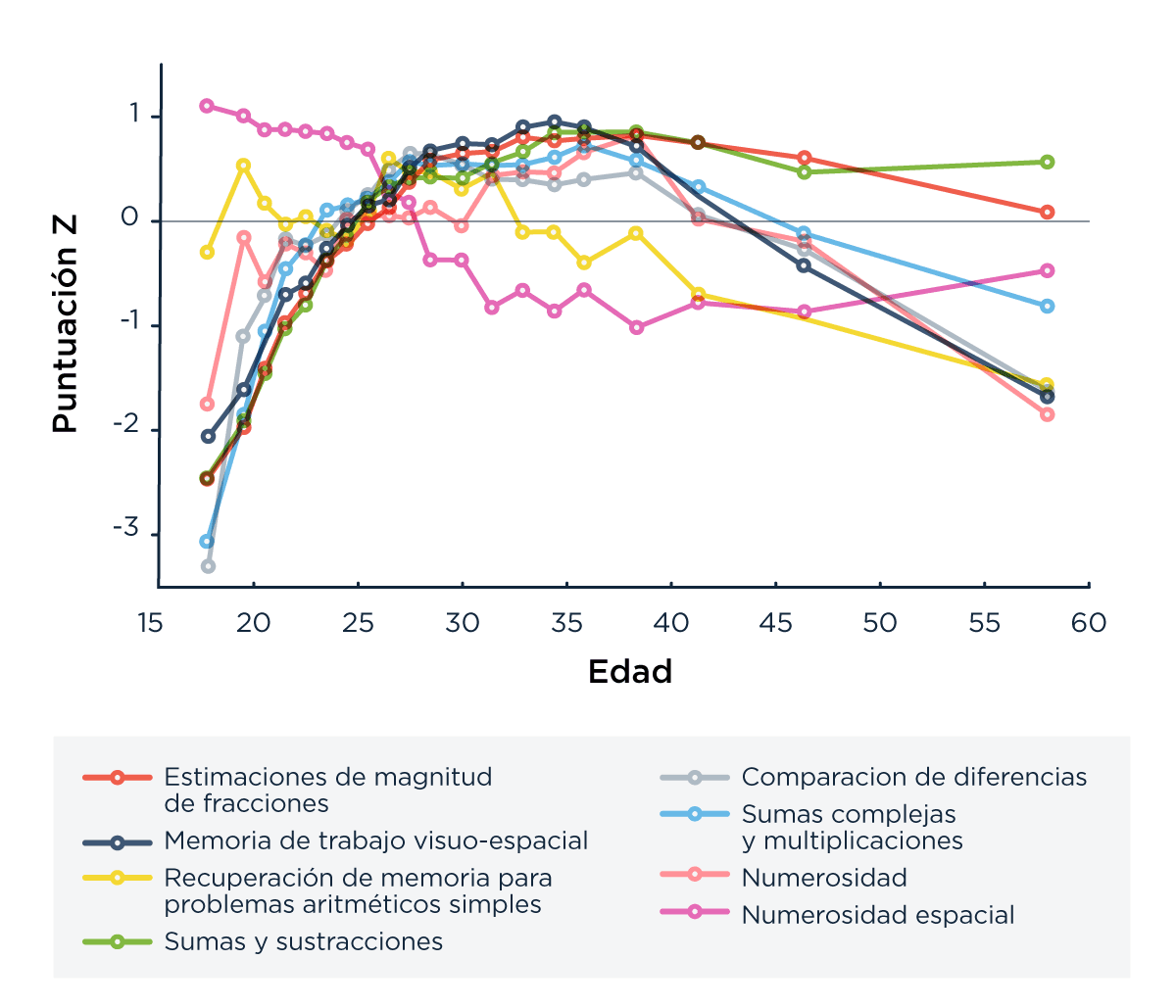
Figura 4: Z-scores como función de la edad para diferentes habilidades. Separamos los participantes en 20 percentiles según sus edades para tener una misma cantidad de datos promediados en cada punto y luego aplicamos un algoritmo de smooth con 5 puntos para mejor visualizar los resultados.
Diferencias de género
Hicimos este análisis usando los datos de todas las personas que respondieron varón o mujer en la pregunta sobre su género (frente a la tercera posibilidad, “otro”): 19.993 de las 22.221 que respondieron las 23 preguntas. Todos los grupos de preguntas presentaron diferencias de género significativas en cuanto al desempeño, salvo el de memoria simple (Figura 5). Los varones tuvieron mayor desempeño en todos los grupos de preguntas, excepto en numerosidad, y la mayor diferencia entre varones y mujeres se vio en, justamente, estimación de fracciones y memoria visuo-espacial.
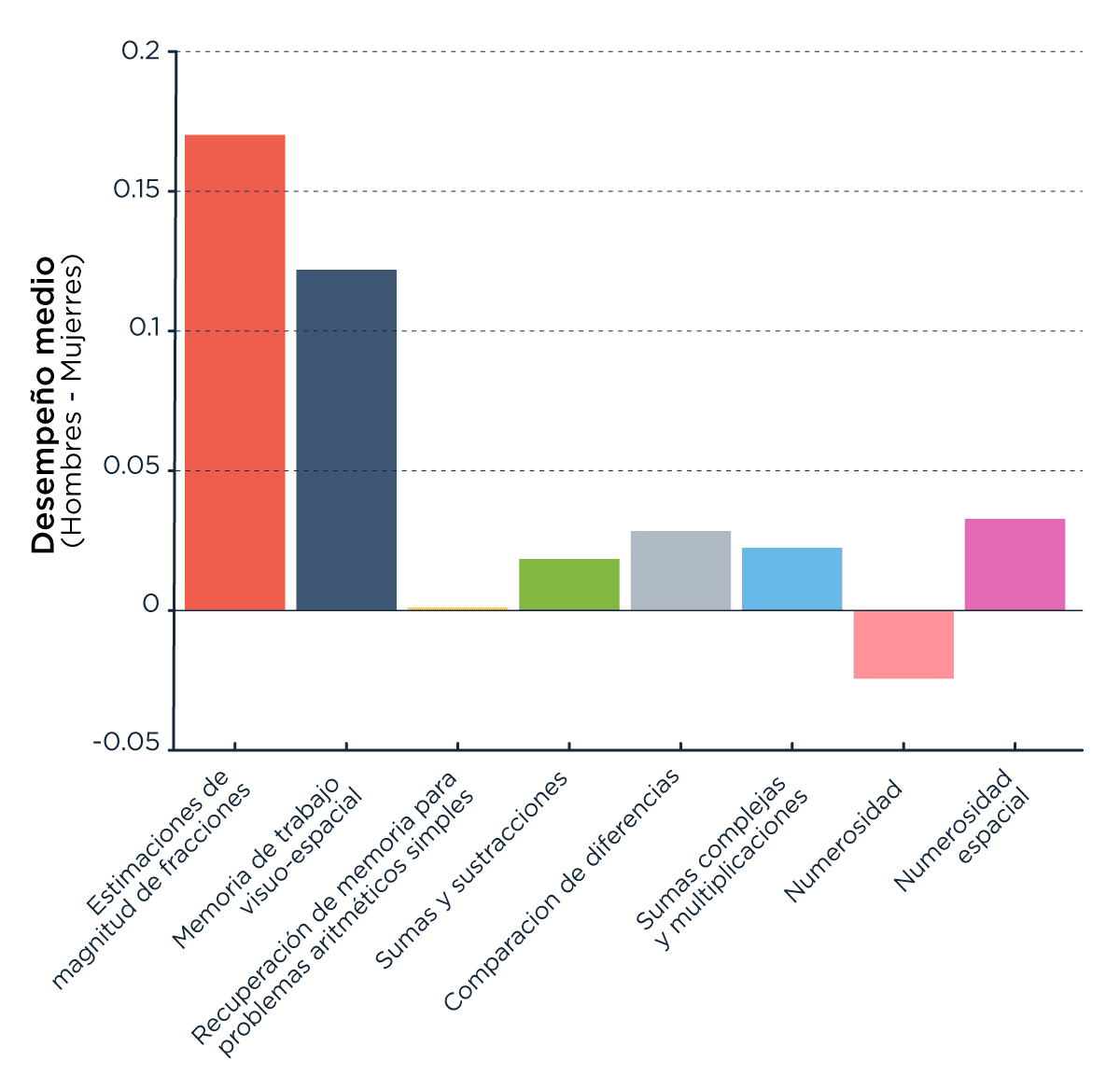
Figura 5: Diferencia de género por grupo de pregunta. Todas fueron estadísticamente significativas.
Regresión múltiple polinomial
Basándonos en los resultados anteriores, simulamos un modelo en el que asumimos que el desempeño depende linealmente de la educación y el género y parabólicamente (mediante un polinomio de segundo orden) de la edad, que, además, es considerada en escala logarítmica.
El resultado detallado de las regresiones lo encuentran en las tablas, pero resumiendo, vimos que:
- Las tres variables (edad, educación y género) influyen significativamente en el desempeño en todos los grupos de preguntas, salvo en tres casos: ni la numerosidad ni la numerosidad espacial parecen depender del nivel educativo, ni las operaciones de memoria simple del género.
- La dependencia de la estimación de fracciones en relación a la edad y al género es muy parecida a la dependencia de la memoria visuo-espacial en relación a esas dos variables (es decir, los correspondientes coeficientes de las regresiones en la Tabla 2 son similares). Sin embargo, la dependencia de la estimación de fracciones en relación al nivel educativo es más parecida a la dependencia de los cálculos complejos en relación al nivel educativo.
Este segundo punto es particularmente relevante a la hora de dar sustento a la hipótesis de la doble representación de fracciones: muestra que a medida que nos educamos podemos estimar la magnitud de una fracción con más precisión, simplemente porque cuesta menos hacer la cuenta. Por el contrario, si no podemos hacer la cuenta, nos basamos en estimaciones que utilizan circuitos perceptivos visuo-espaciales que tienen una menor dependencia con el nivel educativo.
Discusión
Tanto el análisis de grupos como las regresiones sugieren un fuerte solapamiento entre los circuitos cerebrales para la memoria visuo-espacial y para la estimación de porcentajes. En contraste, la numerosidad parece estar disociada. Es, incluso, la única habilidad matemática cuyo desempeño no mejora con el nivel educativo y que muestra una diferencia de género con las mujeres teniendo un desempeño mayor que los varones. También, el hecho de que un análisis multivariado mostró que, cuando controlamos por la edad, la estimación de fracciones muestra una dependendencia similar con el nivel educativo al que muestran los cálculos complejos (y no la memoria visuo espacial), provee evidencia confirmatoria para la teoría de la doble representación de fracciones [Jacob, 2012].
Una observación adicional da sustento a nuestra teoría: la pregunta que mayor poder predictivo tuvo sobre la pregunta 15 es la pregunta 18 y viceversa. La 15 pedía que se estime el porcentaje de alumnos que faltaron a una clase (“En una clase con 30 estudiantes, el día que faltan 6 el porcentaje de ausente es:”). La 18 te mostraba un cuadrado parcialmente pintado y te pedía que estimes qué porcentaje estaba pintado.
Todos los datos y los códigos en matlab que utilizamos para hacer los análisis y los gráficos aquí presentados están disponibles acá. Como todo lo que hacemos en Labs, esta investigación fue posible gracias a las miles de personas que participaron en el experimento y lo compartieron masivamente. ¡Aguante la ciencia colectiva!
Por si querés más detalles sobre los métodos
Participantes
Un total de 22.221 participantes (varones: 10.192, mujeres: 9.012, no especificado: 2297) terminó el test en un tiempo promedio de 7,6 minutos (error estándar 13 sec): 1098 participantes empezaron pero no terminaron el test y fueron excluidos del análisis. Todos los participantes fueron informados de que sus datos anonimizados, colectados a través de internet y celulares inteligentes, serían utilizados para investigación.
Los datos crudos pueden bajarse acá. La Tabla 1 muestra los valores obtenidos para la edad pico de desempeño en diferentes habilidades de acuerdo al un mecanismo de bootstrap [Germine, 2011].
Diseño experimental
Implementamos un test vía web fuertemente basado en tests diseñados para detectar dificultades desproporcionadas en el aprendizaje de la matemática (discalculia). El test consistía de 23 preguntas multiple choice, con tres posibles respuestas cada una. Las autoras de este trabajo somos activas divulgadoras científicas en Argentina, con presencia en redes sociales y medios audiovisuales y escritos, lo que nos permitió una amplia diseminación del experimento, además del increíble empuje de la comunidad de El Gato y La Caja, cuyo alcance es responsable de la mayor parte de las respuestas obtenidas.
Para maximizar nuestra llegada, diseñamos una aplicación amigable y de fácil uso. Experiencias previas con experimentos vía web nos habían mostrado la importancia de la gamificación y de un diseño cuidado para la experiencia del usuario para incrementar el número de participantes que se entusiasman con el experimento [Rieznik 2017, Zimmerman 2016]; este aspecto de la toma de datos online es también enfatizado por otros grupos de investigación usando paradigmas similares [Hartshorne, 2015; Hartshorne, 2018]. Los datos se colectaron en cuatro períodos de tiempo separados cada uno aproximadamente por dos semanas.
El test
Los ítems y posibles respuestas se muestran en este mismo apartado. Los ítems 1, 6 y 14 evalúan la habilidad de comparar valores numéricos, se basaron en Moyer and Landauer [Moyer, 1967] y en un subconjunto del test NUCALC (Neuropsychological Test Battery for Number Processing and Calculation in Children) [Aster, 2000]. Los ítems 2, 3, y 5 se relacionan a la aritmética mental y evalúan habilidades de conteo y de resolución aritmética de sumas y sustracciones simples. Fueron adaptadas del test BAS (British Ability Scale) [Elliot, 1997] y de un subconjuntos del Wide Range Achievement Test III [Jastak, 1993]. Las preguntas 4, 7-13, 15, and 18 son problemas aritméticos situacionales, es decir, imbuidos en un contexto. del test NUCALC y un subconjunto del test Number Sense Core [Jordan, 2007]; las preguntas 15 y 18 requieren la evaluación de porcentajes. Las 16, 17 y 23 miden la habilidad de estimar el número de elementos en un conjunto [Dehaene, 2004]. Se basan en el test “perceptual quantity estimation” de NUCALC [Aster, 2000]. Los ítems 19, 20, 21 y 22 evalúan la percepción visuo espacial y fueron tomadas del test Rey–Osterrieth complex figure [Kosc, 1974] y del Block Design subtest of the Wechsler Adult Intelligence Scale III [Wechsler, 1997], adaptados para su uso online. La pregunta 19 incluía, además de una percepción visual, una estimación de porcentaje.
Agradecimientos
El genio de Fernando Gama nos dio una mano enorme con el análisis de grupo. De hecho, usamos sus códigos en matlab, de donde sale, por ejemplo, el dendograma que mostramos. Mauro Escudero se puso al hombro el desarrollo del test. Sin su colaboración, este trabajo no hubiera sido posible.