| Nombre | @ de twitter | # de Tuits | Seguidores | Bloque |
| Fernando A. Iglesias | FerIglesias | 97.375 | 262.559 | PRO |
| Gabriela Cerruti | gabicerru | 56.700 | 201.912 | FpV |
| Victoria Donda Perez | vikidonda | 47.140 | 189.435 | LIBRES DEL SUR |
| Araceli Ferreyra | aracelidiputada | 43.444 | 4.032 | PERONISMO PARA LA VICTORIA |
| Karina Banfi | KBanfi | 41.085 | 11.574 | UCR |
| Raul Perez | Raul__Perez | 28.520 | 10.400 | UNA |
| Daniel Filmus | FilmusDaniel | 25.370 | 320.719 | FpV |
| Horacio Pietragalla | pietragallahora | 25.118 | 35.128 | FpV |
| Toty Flores | TotyFlores | 22.613 | 26.580 | COALICION CIVICA |
En The Tower and The Square, Niall Ferguson propone recorrer la historia usando una perspectiva de redes como protagonista. Particularmente, una historia donde el entramado social es tan (o más) relevante que el institucional formal. Así, continúa siendo clave para el análisis quién es Presidente, Ministra o Embajador −la arquitectura institucional formal−, pero también empieza a pesar el fútbol de los jueves que comparten el Secretario de Defensa con un contratista privado, o que tanto la Ministra de salud como la de educación disfrutan las películas de terror de los años 50 al punto de postear en los mismos foros.
De esta manera, las redes humanas que se tejen por fuera de lo institucional se vuelven protagonistas a la hora de descifrar procesos que pueden permanecer ocultos si son iluminados exclusivamente con información que proviene de fuentes tradicionales.
En The Salons Letters, la Universidad de Stanford reconstruyó las relaciones personales de los salonnières, intelectuales notables europeos de entre 1700 y 1914, tratando de complementar la aproximación tradicional a la historia con una perspectiva de redes definida por las personas y no por las instituciones. Para eso usaron gran cantidad de cartas, convirtiendo a cada autor en un nodo y cada intercambio en una arista que define una relación.
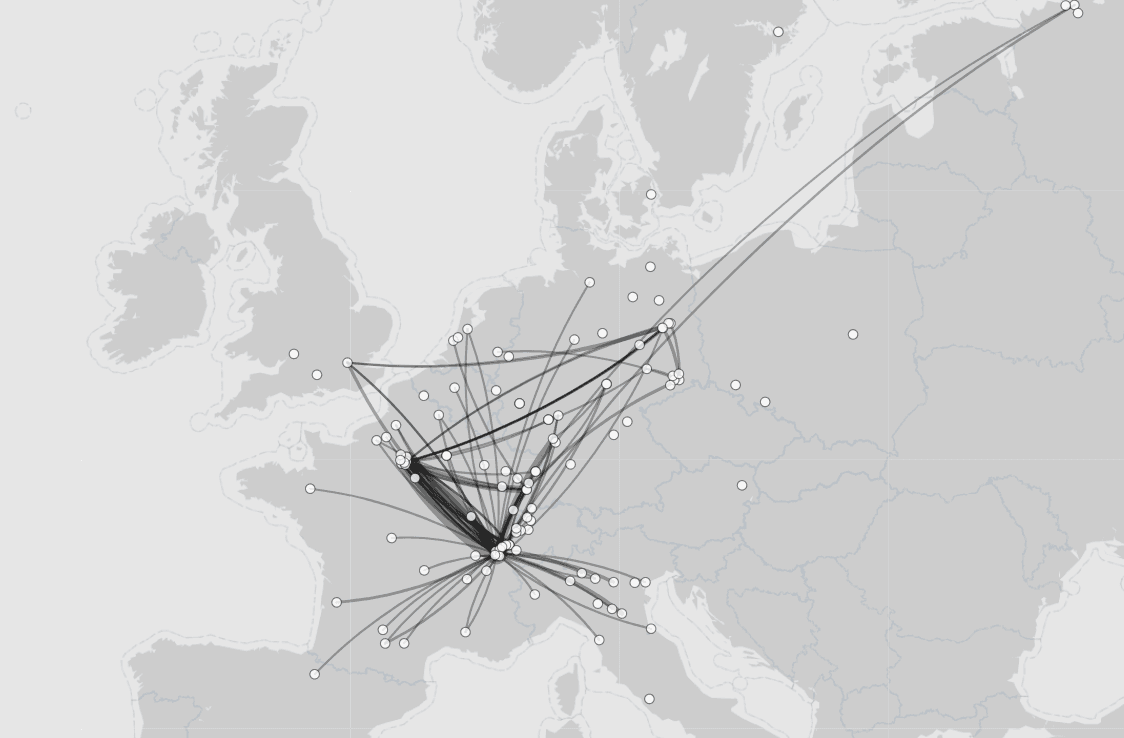
En otro proyecto, reconstruyen las relaciones epistolares de John Locke, tratando de extraer insights que no habían sido observables hasta el momento.
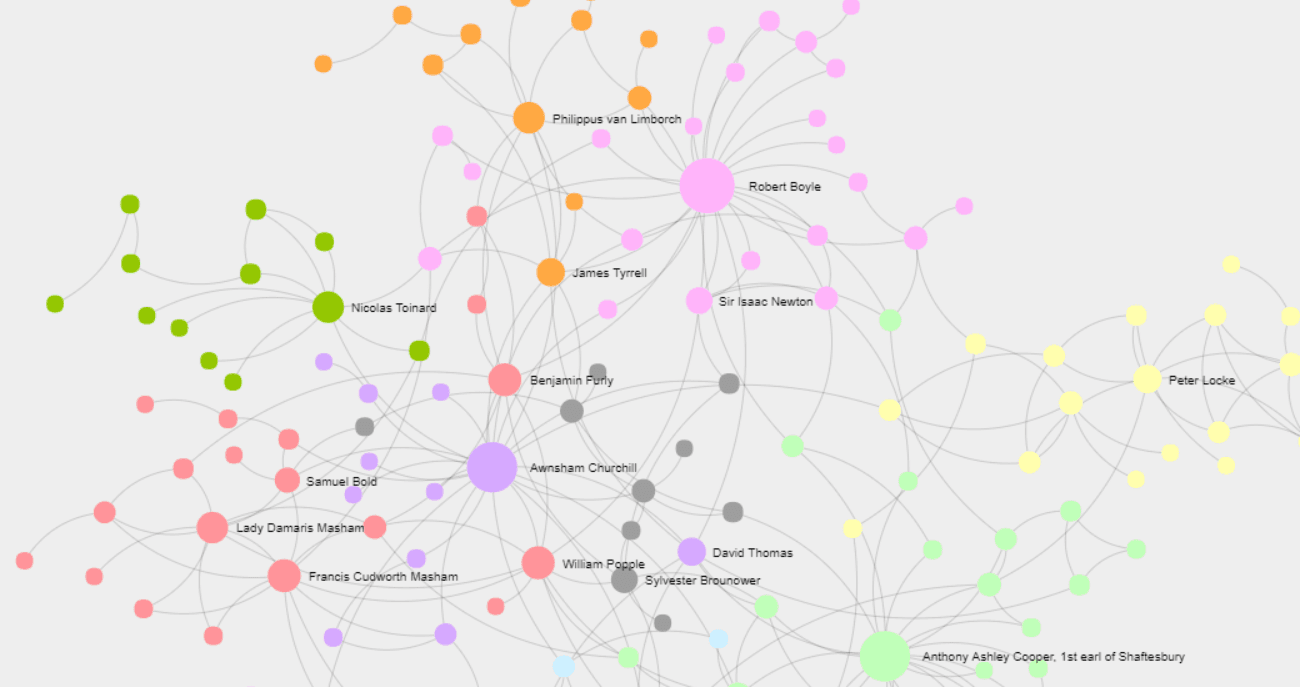
Pero ni todas las redes pasan a puertas cerradas ni tenemos que esperar 100 años para reconstruirlas. Hoy los intercambios epistolares son más bien pocos y conseguir el historial de WhatsApp, o aunque sea la metadata de 256 diputados en ejercicio, no está dentro de nuestras posibilidades actuales (aunque qué divertido ser historiador del futuro). Por suerte, existen otros intercambios que, lejos de ser privados, ‘se esconden’ a plena vista, por lo menos hasta que los ordenamos todos en una sola imagen.
Hace apenas una semana, Economía Feminista proponía llenar una planilla compartida con información sobre nuestra actual cámara de diputados:
Al verla, inmediatamente nos hicimos la pregunta de si podíamos tratar de visualizar la estructura de relación entre los diputados usando información pública disponible en Twitter y ver qué pasaba con esa estructura cuando agregábamos los datos de la discusión sobre el aborto.
Arranquemos por el principio.
Una red pública de Diputados
Lo primero que nos preguntamos es cómo nuestros representantes legislativos se hablaban y se escuchaban los unos a los otros en Twitter. Para eso, generamos un grafo donde cada diputado es un nodo y, ante cada par, establecimos una relación direccional. Así, si el diputado A sigue a la diputada B, habrá una arista (la línea que los une, que estrictamente es una flecha) con una dirección que parte de A y llega a B. Hicimos esto con todos y cada uno de los 237 diputados que tienen cuenta de Twitter (al mismo tiempo que nos preguntamos qué onda los que no, o más bien qué onda los equipos de comunicación de los que no). EMOJI PENSATIVO DE REDES.
Antes de seguir adelante nos pusimos a ver las limitaciones del dataset, o por lo menos una descripción que nos orientase respecto de qué tan ‘buenos’ eran los datos y que explicitara las limitaciones de interpretación de ahí para adelante, que por supuesto son unas cuantas y es importante tenerlas enfrente.
Primero, nos fijamos qué tan tuiteros eran nuestros diputados, con un usuario que se despega del pelotón con casi 100.000 tuits emitidos (y, dato al paso, solamente 11 favoritos sobre tuits ajenos): el diputado Fernando Iglesias.
Completan el top 10 de tuiteros recurrentes que además son diputados:

Para los que preguntan ‘¿no habría que poner eso en una logarítmica?’, la respuesta es sí.
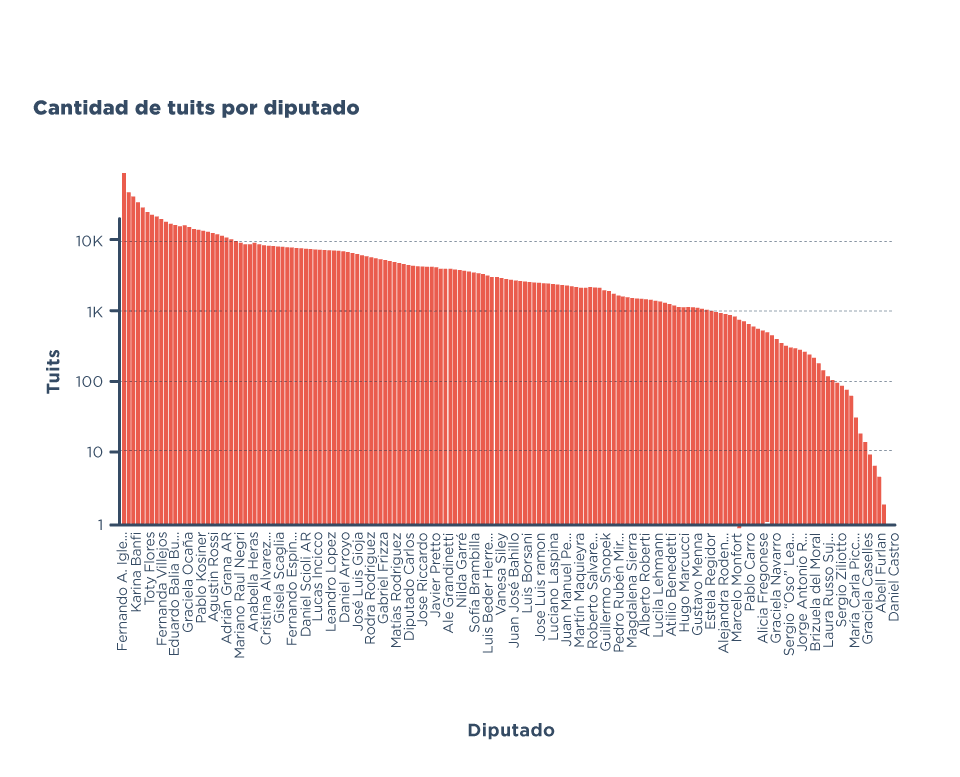
Esto nos muestra una progresión más o menos esperable, y un puñado de diputados que medio que se abrieron una cuenta de Twitter y no le dieron tanto uso, con mención de honor a las diputadas María Isabel Guerin, Mirta Pastoriza y Daniela Castro, que tienen un total agregado de 0 tuits.
¯\_(ツ)_/¯
Igual, el top 10 que más de uno debe querer ver es el de seguidores:
| Nombre | @ de twitter | # de Tuits | Seguidores | Bloque |
| Daniel Scioli | danielscioli | 7.594 | 1.451.073 | FpV |
| Martín Lousteau | GugaLusto | 3.673 | 1.113.238 | EVOLUCION RADICAL |
| Elisa Lilita Carrió | elisacarrio | 8.039 | 1.033.031 | COALICION CIVICA |
| Axel Kicillof | Kicillofok | 2.274 | 675.344 | FpV |
| Daniel Filmus | FilmusDaniel | 25.370 | 320.719 | FpV |
| Fernando A. Iglesias | FerIglesias | 97.375 | 262.559 | PRO |
| Juan Cabandié | juancabandie | 4.320 | 207.531 | FpV |
| Gabriela Cerruti | gabicerru | 56.700 | 201.912 | FpV |
| Victoria Donda Perez | vikidonda | 47.140 | 189.435 | LIBRES DEL SUR |
| Graciela Ocaña | gracielaocana | 16.569 | 185.224 | PRO |
La respuesta a ‘¿Y cuántos de estos son fake?’ la pueden buscar uno a uno ustedes mismos acá y, spoiler alert, no los sorprenderá.
El Grafo
Con todo esto en mente, construimos un grafo a partir de 237 nodos y 5.291 interacciones entre ellos. Esas interacciones se dan entre cada par de puntos, y no están informadas de ninguna manera sobre los partidos de los puntos, sobre si los dos puntos que unen son del mismo partido o no. Acá es donde las cosas empiezan a ponerse divertidas.
Primero, tenemos 6 diputados que se caen del mapa (estrictamente, ‘no se relacionan con la componente principal’): Alma Chani Sapag, Lorena Matzen, Mirta Pastoriza, Carlos Selva, Hugo Infante y Juan Antonio Silva no siguen o son seguidos por ninguno de sus compañeros de trabajo en Twitter.
Ahora, con la red de los conectados y sin darle al software más información que ‘este se relaciona con este de esta manera’ para todos los pares de puntos, le pedimos que los ubicara en el espacio de manera de balancear dos fuerzas contrapuestas, una que los aleja y una que los acerca.
Así:
- Cada punto repele a todos los demás como si fuese una partícula cargada eléctricamente.
- Cada punto se atrae con otro gracias a los vínculos que existen entre ellos como si un resorte tirase de la unión.
Nada más. Ni información de partido, ni de postura, NADA. Este fue el primer resultado:
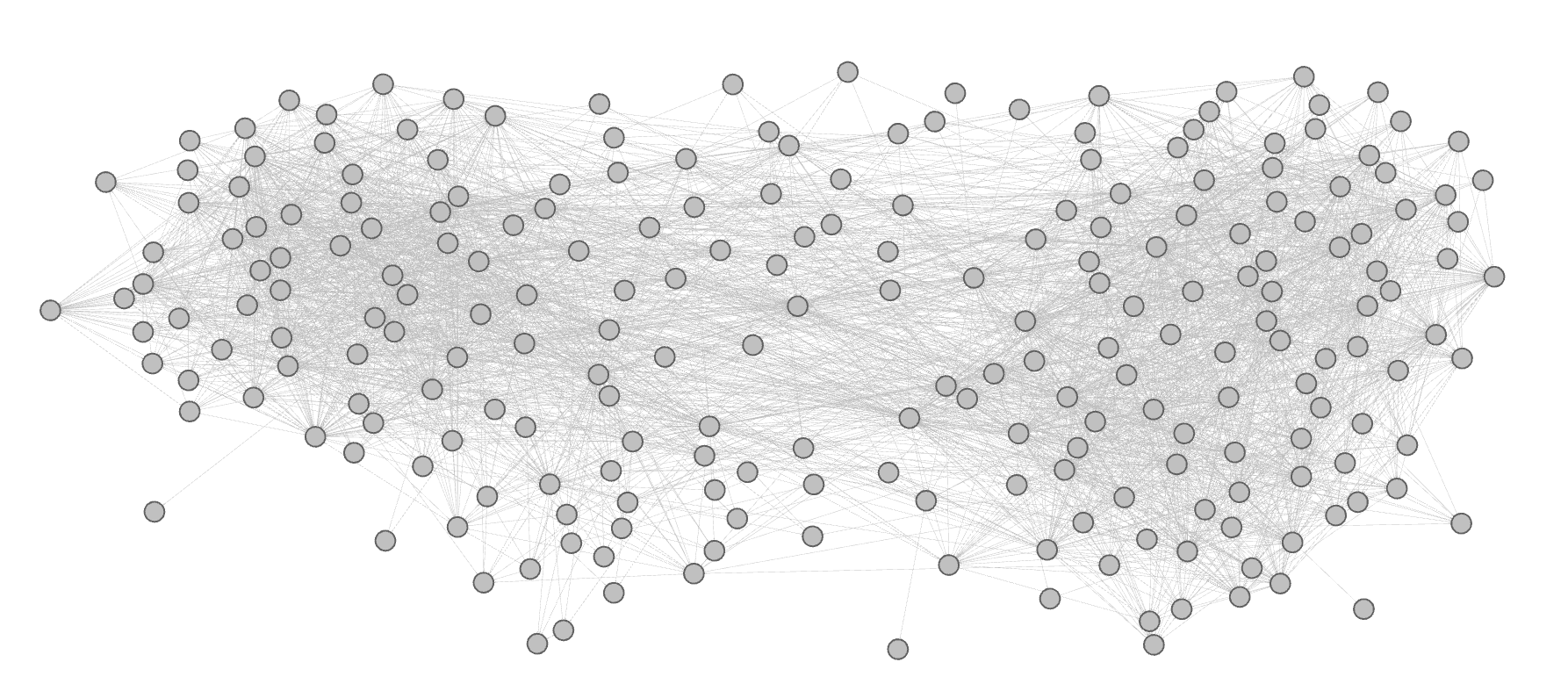
De esta forma, se vuelve evidente que existe algún tipo de orden en esta estructura. No todos los nodos muestran la misma probabilidad de relacionarse con otros, y esto nos hizo pensar en varias cosas. La primera fue que, si bien es completamente esperable que una red humana se estructure de alguna manera distinta de todoscontodos, hubiese sido hermoso que así pasara para este caso particular. Por esto queremos decir que, pese a que las personas tendemos naturalmente a agruparnos por afinidad −y esas estructuras se reflejan directamente en nuestras redes sociales−, qué ganas de descubrir que nuestros representantes políticos hacen un esfuerzo por trascender eso y buscan activamente recibir información ‘del otro lado’ y exponerse a posturas distantes de las propias (y de las de su partido).
Bueno, medio que eso no pasó.
La pregunta que se nos presentó inmediatamente después fue si de una estructura generada a partir de un dato tan pequeño como ‘este sigue a este otro en Twitter’ se podría, de alguna manera, extraer información relevante sobre los participantes, como por ejemplo si podríamos adivinar las pertenencias partidarias basándonos únicamente en esas relaciones.
Para esto, tratamos de dividir ese grafo en unidades definidas más pequeñas; de nuevo, no a partir de etiquetas que nosotros pusiéramos a priori, sino sólo usando sus relaciones.

Esta estructura (que no es única sino que pueden generarse distintos números de comunidades dependiendo de cómo se ajusten los parámetros de la segmentación), nos dividía a los participantes en 5 grupos principales, a los que pintamos con los colores predeterminados que ofrece la aplicación (así nos evitamos todos precipitar una conclusión en base a ellos).
Aún así, es divertido tratar de adivinar, primero, si la información que estamos viendo es de alguna manera relevante (o sea, si se solapa con la realidad o nos permite hacer inferencias sobre ella) y, segundo, cuáles nos imaginamos que pueden ser cada una de esas fuerzas políticas.
Inmediatamente después, en lugar de usar la información que emerge de cómo se relacionan, decidimos pintar los nodos por bloque político y cruzar los dedos deseando que diera algo más o menos parecido.

¿Perfecto? No, pero

O sea que, si bien los grupos que se forman analizando solamente la estructura de conectividad (que, de nuevo, ni siquiera es una estructura muy compleja sino que es simplemente seguido/seguidor, y que podría mejorar MUCHÍSIMO agregando otros parámetros como actividad de retuiteo, menciones cruzadas, similitud en el discurso, etc.), la red es informativa y nos permite visualizar relaciones con un solo golpe de vista.
Endogámicos
Al ver estas estructuras, otra pregunta que nos hicimos fue qué partidos eran más endogámicos. O sea, qué fuerzas políticas se exponían potencialmente a más opiniones de copartidarios y a menos ideas delotrolado (y decimos ‘potencialmente’ porque de seguir a alguien en Twitter a leerlo con atención y considerar que su postura es interesante hay largo trecho). Para eso tomamos dos caminos: una aproximación gráfica preciosa y una analítica, mucho menos bonita quizá, pero más precisa. Así, ordenamos en una disposición circular a todos los diputados y graficamos con aristas pintadas del color de origen cada vínculo, lo que nos mostró esto:

Podemos ver que se hace más clara la cuestión endogámica, y hasta pareciera ser mayor en el FpV que en otros partidos, pero mejor medirlo en forma analítica que a ojo. Para eso, calculamos la matriz de mezcla, que nos da una medida de qué tan estructurada está una red (o, en este caso, qué tan endogámica es la estructura de comunicación en Twitter de nuestros diputados).
Lo que encontramos es que los bloques más grandes son, también, los más endogámicos (para la comunicación, en Twitter, con los supuestos y limitaciones que ya contamos).

Esta matriz indica cuánto se siguen los diputados de los diferentes bloques entre sí, tanto para adentro del bloque como para afuera. Para leerla comenzamos por la primera fila, que nos dice que de las personas que alguien del FpV sigue, en promedio a 80% son de su propio bloque (resultado muy por encima del esperable por azar, sabiendo que representan el 25% de los diputados) . Lo mismo pasa con el PRO en un 62% (22% de los totales) y la UCR en un 47% (sobre una base del 16%); y se ve un cruzado muy interesante entre FpV y Justicialismo.
En este punto podríamos decir que ‘nada mejor para un peronista que otro peronista’, pero con frenteparalavictoria queda larguísimo. Además, si comparamos la cantidad de sobrerepresentación de tu propio bloque sobre el total, el FpV termina en 3,2 veces (80%/25%), y tanto el PRO como la UCR muy cerca de 3 (2,8 y 2,9 respectívamente).
Lo relevante en esta figura es ver a diagonal, que nos cuenta un poco la historia de una homofilia anunciada donde se entreteje más hacia adentro de lo que se expone a información de afuera.
Para ver si había influencia de género hicimos lo mismo, pero esta vez respecto de esa característica, y lo que vimos fue lo siguiente):

Esta matriz indica cuánto se siguen los varones y mujeres diputados y diputadas entre sí. Para leerla comenzamos por la primera fila, la cual indica la probabilidad de que un varón siga a otro varón o a una mujer. Esta magnitud depende totalmente de la proporción que existe en la población (61% diputados varones, 39% mujeres). O sea, tanto varones como mujeres tienen un ligero sesgo a seguir a más varones que la representación poblacional, pero es muy ligera esa diferencia.
Podemos ver ese mismo fenómeno de otra manera, acá:

MetaGrieta
Pero esa no era la pregunta que nos picaba, o no por lo menos esta vez. Lo que queríamos averiguar era cómo se veía esta red cuando lo que usábamos para asignar los grupos no era la pertenencia política sino la postura ante el aborto seguro, legal y gratuito, y si agregar esta información nos daba alguna pista sobre los diputados que todavía no se pronunciaron.

¿La Grieta? Emasomeno. ¿Hay tendencias generales que muestran que un bloque exhibe principalmente una postura? Claro que sí, pero está lejos de monolítica, y aparecen todos esos puntos grises tan interesantes (e importantes): los no definidos.
La pregunta es cómo llegarles a esos no definidos, o por lo menos aventurarnos un poco pensando si, dados los datos que podemos ver, es posible usar Twitter para indagar qué piensan y entender qué ve cada uno de acuerdo a quién sigue e inclusive cuáles de nuestros diputados (y bloques) escuchan más por fuera de los suyos.
Entonces, lo primero es entender qué tan expuestos están nuestros representantes públicos a las opiniones de sus compañeros. Para eso, graficamos el diámetro de los nodos de forma proporcional a su Out Degree, es decir, a cuántos de los otros nodos siguen:

Muy bien 10 felicitado para Ezequiel Langan, del PRO, que sigue a 105 de sus compañeros. El ranking se completa así:
| Diputado | ¿A cuántos otros diputados sigue? | Bloque |
| Ezequiel F Langan | 105 | PRO |
| Daniel Kroneberger | 86 | UCR |
| Brenda Austin | 79 | UCR |
| Mayda Cresto | 74 | JUSTICIALISTA |
| Horacio Goicoechea | 73 | UCR |
| Daniel lipovetzky | 68 | PRO |
| Sofia Brambilla | 68 | PRO |
| Carla Carrizo | 67 | EVOLUCIÓN RADICAL |
| Karina Banfi | 65 | UCR |
| Soledad Carrizo | 65 | UCR |
Pero, para este caso, nos interesa el de los que escuchan pero todavía no están decididos.
| Diputado | ¿A cuántos otros diputados sigue? | Bloque |
| Ezequiel F Langan | 105 | PRO |
| Daniel Kroneberger | 86 | UCR |
| Astrid Hummel | 62 | PRO |
| Wado de Pedro | 57 | FRENTE PARA LA VICTORIA - PJ |
| Andrés Larroque | 40 | FRENTE PARA LA VICTORIA - PJ |
| Carolina Moises | 40 | JUSTICIALISTA |
| Pablo Torello | 36 | PRO |
| Yanina Gayol | 36 | PRO |
| Martin Perez | 34 | FRENTE PARA LA VICTORIA - PJ |
| Alicia Soraire | 31 | FRENTE PARA LA VICTORIA - PJ |
Listo, tenemos a los receptivos (o algo así).
Llegado este punto, podemos hacernos otras preguntas, como por ejemplo quiénes son nuestros diputados influencers, no definidos por cuántos de sus compañeros los siguen, sino también por cuál es la posición de sus seguidores en la red. Así, buscamos influencia sobre la estructura completa (los 237 dipus), en lugar de solamente sobre los adyacentes. De las medidas que podíamos elegir, tomamos el algoritmo de PageRank, que mide ‘importancia’ como un reflejo de la cantidad de caminos por los cuales ‘caés’ en un nodo particular más frecuentemente. En este caso, lo pensamos como ‘Tuits de quién es más probable que vea seguido, dado que forma parte de esta red’, y así nos quedamos con nuestros dipfluencers (?):

Qué picante va a estar esto con usuarios pesados como Lilita Carrió, Daniel Scioli y Fernando Espinoza empujando los no desde lugares distribuidos y Mario Negri, Fernando Iglesias, Juan Cabandié, Axel Kicillof, Victoria Donda y Cristina Álvarez Rodríguez del lado del sí.
Hoy el proyecto por el aborto legal, seguro y gratuito se propone en diputados y todos los ojos van a estar en nuestros representantes. Difícilmente haya días más importantes para meterles presión para que se expresen públicamente respecto de cómo ejercen esa representación, para que podamos elegir si votarlos o no la próxima vez.
Que sepan que puede haber mil redes privadas, mil llamados, mil reuniones a puertas cerradas, pero que no por eso crean que no los estamos mirando.
BONUS
Acá, imágenes grandes de todo:


Y, lo más divertido, el gif:

NOTA: Todos los grafos fueron actualizados ayer 5 de marzo por la noche. Vamos a ir actualizando a medida que entre información nueva. Para eso, de nuevo recomiendo que participemos todos en agregar esa información, que está disponible de forma pública acá: https://docs.google.com/spreadsheets/d/1mOiTT3JIdQPxVLTQ-a3OivQqE15oLvdWMv6I_DpMZak/edit?ts=5a91f1d7#gid=284647062




