¿Por qué miras la paja que hay en el ojo de tu hermano
y no ves la viga que está en el tuyo?
(Lucas 6, 41-42)
Qué inesperado arrancar con una cita bíblica. Qué impensado, qué inadecuado. Qué inconsistente.
Los humanos no somos grandes razonadores, pero somos buenos para lo que se conoce como detección de trampas y definitivamente nos importa la reputación de cada persona. La obsesión con la coherencia ajena parece doblemente estimulante: detectar incoherencias es fácil y nos permite elaborar juicios sobre la reputación de otros. Pero ¿hay algo más allá de esta satisfacción en deschavar problemas de los demás?
En general, no cuestionamos la idea de que es bueno ser coherente. ¿Por qué está mal creer que llueve y que afuera no llueva; o creer que mañana va a ser un lindo día a pesar de que mañana es martes y todos los martes son feos?
Una respuesta posible es que no hay respuesta. Ser incoherente está mal y listo. Pero algunos filósofos y científicos se tomaron en serio el problema e intentaron darle respuestas más convincentes y menos dogmáticas. Como casi siempre en filosofía, nadie está convencido de nada (salvo Descartes, que cogito ergo sum). Pero, para los que no somos fans de la seguridad como el ubicuo dualista, los argumentos que proponen desconfianza al valor intrínseco de la coherencia son buenos y merecen que les prestemos atención.
Aristóteles, el práctico
El primer filósofo en tomar en serio la pregunta por la incoherencia fue Aristóteles. En su libro 4 de Metafísica, Aristóteles observa que si creemos que hay un precipicio, y no hay un precipicio en el camino, no podemos decidir si caminar o no. Es decir, un pensamiento contradictorio nos genera una parálisis en la acción.
De forma mucho más prolija, el brillante economista/filósofo/matemático Frank Ramsey sugirió en 1926 −a sus 24 años (dato acompañado por el silencio de la autoexaminación de logros personales y, tal vez, el sonido de un corchazo)− el argumento de Dutch Book (literalmente ‘apuesta holandesa’, pero sería una ‘apuesta tramposa’). La idea es que si tenemos un conjunto irracional de creencias, deberíamos entrar en apuestas donde siempre (pase lo que pase) estamos condenados a perder plata.
Supongamos que alguien viene y te propone la siguiente apuesta: ‘Si hoy gana Boca, te doy $100; si no gana, no te doy nada’. Pero esa apuesta tenés que comprarla. ¿Cuánto pagarías? Depende cuán confiado estés en que gane Boca, pondrás más o menos dinero. Si tu confianza fuera 0.1, es decir, si creés que hay un 10% de chances de que gane Boca (supongamos que juega contra Real Madrid), no pagarías $80 por esa apuesta, sino mucho menos. Según Ramsey, si fueras racional pagarías $10 o menos por la apuesta en cuestión. Este supuesto se mantiene en prácticamente toda la teoría de la decisión (que justamente nació en 1926 con el artículo de Ramsey).
Hay muchos requisitos de racionalidad. Acá sólo vamos a mencionar uno sencillo: si creés A en grado x, tenés que creer ¬A (‘no es cierto A’) en grado 1-x. Es decir, que si creés que hay 40% de chances de que llueva, creés que hay 60% de que no llueva. Si creés 0.9 que Argentina clasificará para el próximo mundial (seamos optimistas!), creés en 0.1 que no clasificará. Bastante obvio. Ahora viene la parte de mostrar que si no cumplís este requisito, estás condenado a perder plata.
El resultado de Dutch Book nos muestra que una asignación no-probabilística nos va a provocar una apuesta de pérdida segura. Por ejemplo, supongamos que uno cree que ganará Boca en grado 0.6 y cree que no ganará Boca en grado 0.7 (por “no ganar” entendemos perder o empatar).

Ganen o no ganen, pero sepamos todos que la probabilidad suma 1.
Según el cálculo probabilístico asignar valores de 0.6 para la victoria y 0.7 para la no-victoria es irracional, porque la confianza en p y ¬p debe sumar 1, no más. Ahora viene un comerciante inteligente y nos vende estas dos apuestas y empieza a negociarnos el precio para cada una:
Apuesta 1:
Si gana Boca, recibís $100
Si no gana Boca, recibís $0
Apuesta 2:
Si no gana Boca, recibís $100
Si gana Boca, recibís $0
Dado que nuestra creencia en que Boca gana tiene grado 0.6, estamos dispuestos a comprar la primera apuesta por $60. Sería ideal pagar menos, pero siguiendo a Ramsey sabemos que $60 ya es un precio razonable. Por otro lado, dado que nuestra creencia en que Boca no gana tiene grado 0.7, compraremos la segunda apuesta por $70. Pero de este modo, nos gastamos $130 en estas dos apuestas. Y pase lo que pase (si Boca gana o no), ganaremos sólo $100. ¡Menos de lo que pusimos! Una catástrofe: habremos perdido un total de $30 en cualquier escenario.
La prueba de Dutch Book es parecida pero más general, porque muestra que cualquier caso de incumplimiento de probabilidades nos llevará a una posible apuesta con pérdida segura. Mucho peor será el caso si creemos directamente en contradicciones (por ejemplo, creyendo p y ¬p en grado 1); en ese caso, será racional apostar $100 por la victoria, y $100 por la no-victoria, para un premio de $100. Es decir, apostaremos $200 por un premio de $100, y terminaríamos perdiendo $100 pase lo que pase en el mundo.
De todos modos, el argumento de Dutch Book suele ser criticado porque supone una relación demasiado directa entre nuestras creencias y nuestra conducta de apuestas. Los supuestos de Ramsey sobre cómo deberíamos actuar respecto a nuestras creencias no son obvios. O capaz los que no somos obvios somos las personas, bah.
¿Realidad? ¿No habían cerrado ya ese antro?
Hay argumentos a favor de la coherencia que no tienen nada que ver con apuestas ni asuntos prácticos. Estos argumentos ‘epistémicos’ nos dicen que las creencias incoherentes están condenadas a un menor contacto con la realidad.
En teoría de la decisión, una acción es claramente irracional cuando hay otra acción que, pase lo que pase, será mejor. Cuando eso pasa decimos que la primera acción (la irracional) está dominada por la otra. Por ejemplo, supongamos que pido un gusto de helado en una heladería que no conozco, y tengo que elegir entre frutilla y dulce de leche. El helado de frutilla me gusta cuando la heladería es buena, pero me horroriza cuando la heladería es mala (nada peor que un helado de frutilla mal hecho). En cambio, el de dulce de leche me gusta muchísimo cuando la heladería es buena, y me da igual cuando la heladería es mala. De este modo, lo racional es pedir dulce de leche, porque pedir frutilla está dominado: no importa si la heladería es buena o mala, siempre va a ser mejor para mí pedir dulce de leche antes que pedir frutilla.
Suele pensarse que, así como las acciones buscan el mayor beneficio posible, las creencias buscan el mayor contacto posible con la realidad. De este modo, si tenemos que decidir qué creer, tenemos que buscar el cuerpo de creencias que nos deje lo más cerca posible de la realidad. Joyce (1998) probó que cualquier cuerpo de creencias que viole los principios de la probabilidad va a estar ‘dominado’ por una asignación probabilística: es decir, hay un cuerpo probabilístico que estará más cerca de la verdad que ese cuerpo no-probabilístico, sea lo que sea que pase.
Para entender informalmente la prueba, podemos pensar en una sola oración p (supongamos ‘Boca va a ganar’) y dos posibilidades: el mundo w1 donde Boca gana, y el mundo w2 donde Boca no gana. El eje horizontal representa nuestro grado de creencia en que Boca ganará (que va de 0 a 1), y el eje vertical representa el grado de creencia en que no ganará (que también va de 0 a 1). La diagonal representa las asignaciones coherentes de probabilidad: es decir, aquellas donde p y ¬p suman 1 (para darse una idea de por qué, piensen en el punto medio del cuadrado, que obviamente está en la diagonal, donde creemos p y ¬p en 0.5).
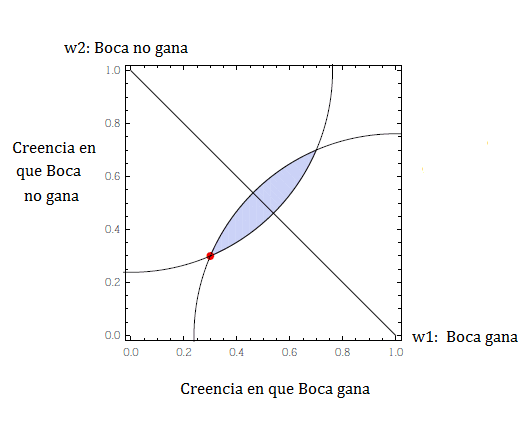
Que te digan que tu modelo de la realidad tiene oportunidad de mejora es una cosa, pero que te lo grafiquen ya es mucho.
Elijamos pensar, por ejemplo, que Boca ganará en grado 0.3, y también creamos que no ganará en grado 0.3. Obviamente esto es incoherente porque me faltan 0.4 para el mango (o para que las condiciones p y ¬p sumen 1). Lo que todavía no tuvimos en cuenta fue la realidad. Si Boca gana (mundo w1), habría muchas asignaciones de probabilidad más cercanas al mundo real que nuestra creencia original: todas las que están dentro del círculo que dibujamos en torno a w1. Por otro lado, si el mundo real fuera w2 y Boca no gana, habría muchas otras asignaciones más cercanas al mundo real (todas las que están dentro del círculo que dibujamos en torno a w2). El área sombreada representa las asignaciones que están más cerca de la verdad en ambos escenarios. Y es fácil ver que dentro del área gris hay asignaciones probabilísticas (las que forman parte de la diagonal). Esas asignaciones probabilísticas dominan nuestra creencia incoherente original: son mejores que nuestra creencia original pase lo que pase en el partido.
El segundo gráfico nos muestra qué pasa cuando nuestra asignación es de hecho coherente o probabilística (supongamos que le damos 0.5 a p y 0.5 a ¬p): como el punto pertenece a la diagonal, no queda ningún ‘área gris’. Es decir, nuestra asignación de probabilidades no queda dominada por ninguna otra asignación. Nuestra creencia podría ser pésima a la luz de los hechos posteriores (en este caso no hay mucho riesgo porque sólo expresamos incertidumbre completa), pero ‘en principio’ no es peor que ninguna otra.
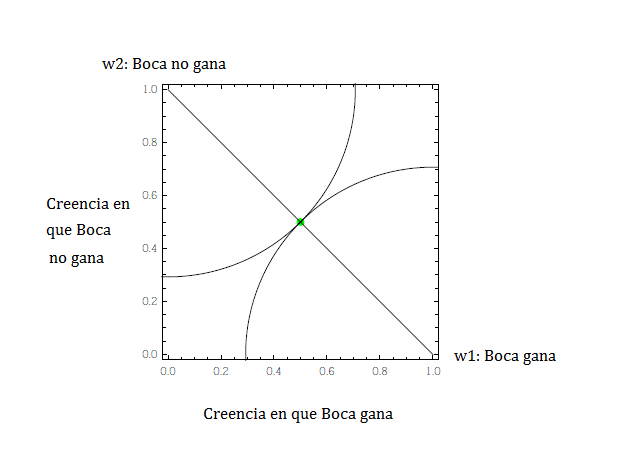
Que lindo, todo racional, sin áreas superpuestas de mejora hacia un modelo probabilístico.
Este argumento (que pueden ver acá generalizado) nos muestra que, en tanto nuestro pensamiento es irracional, siempre podemos encontrar uno racional que será más adecuado (sin importar cómo sea el mundo real). En cambio, si nuestro pensamiento es racional, no puede estar dominado por otro y sólo serán los hechos los que juzguen.
Hasta acá, toda una apología de la racionalidad. Preparémonos para un pero. Como observa Kolodny en su artículo-bomba ‘¿Cómo importa la coherencia?’ (2007), no es claro que el argumento de adecuación de Joyce sea tan decisivo a favor del probabilismo: si bien muestra que cualquier asignación irracional está dominada por una racional, no todas las asignaciones racionales dominan a las irracionales (en términos gráficos, no todos los puntos de la diagonal están en el área gris). Es decir, algunas asignaciones coherentes no son necesariamente mejores que las incoherentes.
Dicho de otro modo, si nos enfocamos en el mundo real y no en las posibilidades, algunas creencias irracionales pueden ser preferibles a otras racionales. Por ejemplo, si el mundo fuera uno donde Boca gana, es mejor creer que gana con probabilidad 0,9 y que no gana con probabilidad 0,2 (donde seríamos incoherentes pero no tanto), que creer que gana con probabilidad 0 y que no gana con probabilidad 1 (donde seríamos coherentes pero completamente errados respecto a la realidad). En teoría, la teoría funciona. En la práctica, ¯\_(ツ)_/¯.
¡No tan rápido, amigo!
A pesar del Dutch Book y los argumentos de adecuación, hay algunos argumentos que indican que la coherencia no es tan importante como parece. De hecho, en algunos casos la incoherencia parece ser la única opción correcta.
1.Paradoja del prefacio.
En su artículo “La paradoja del prefacio” (1965), David Makinson nos pide imaginar a una profesora de historia que escribe un libro luego de un arduo trabajo de investigación. En el prólogo, la profesora dice “Esta investigación es empírica, y naturalmente involucra muchísimos detalles; como tal estoy segura que contiene algunos errores.” En este caso, la profesora considera (razonablemente) que el largo libro tiene algunos errores. Pero al mismo tiempo, cree en cada enunciado del libro, porque le ha llevado décadas de investigación. Es decir, el cuerpo de creencias de la profesora es inconsistente: cree que el libro tiene algunos errores, y al mismo tiempo cree individualmente en cada una de las cosas que escribió. Sin embargo, es (o al menos parece) racional. La paradoja suscitó una decena de respuestas.
Una manera de explicar la paradoja del prefacio es apelando a conceptos probabilísticos. A la luz de la evidencia (es decir, la investigación que hizo la profesora), cada enunciado del libro tiene una probabilidad alta. Sin embargo, si ponemos a los enunciados todos juntos, la probabilidad de ese enunciado general es muy baja. Entonces la inconsistencia puede ser una manera razonable de responder a la evidencia.

De este modo, el protagonista del problema es el principio de Locke, según el cual debemos creer todo lo que tiene probabilidad alta. Si aceptamos este principio (que al menos a primera vista es razonable), estaremos condenados a tener creencias incoherentes.
2.¿Contradicciones verdaderas?
A ciencia cierta, todos los argumentos a favor del probabilismo (Dutch Books o de adecuación) se basan en la idea general de que no puede haber contradicciones verdaderas: los únicos mundos posibles son aquellos donde (por ejemplo) Boca gana, y donde Boca no gana. Lo mismo se aplica para cualquier evento.
Pero si bien este supuesto es aceptado por casi todo el mundo, la lógica contemporánea puede desprenderse de él. De hecho, la teoría dialeteísta de Priest (1987) sostiene que en ciertos casos específicos (oraciones paradójicas como ‘esta oración es falsa’, fenómenos cuánticos extrañísimos, etc.) podría haber contradicciones verdaderas. Esta teoría se basa en la lógica LP (por Lógica de las Paradojas), creada casi como una curiosidad por el lógico argentino Florencio Asenjo en 1966. El sistema lógico LP es perfectamente aceptable como lógica (tiene tautologías, inferencias, reglas) pero no admite el principio de no-contradicción. Esto refuta la idea común de que la lógica depende de la no-contradicción.
Naturalmente, si el mundo fuera contradictorio, tener un sistema incoherente de creencias es lo más razonable. Pero claro que este es un supuesto muy fuerte, y por varias razones nos conviene seguir creyendo que el mundo no tiene contradicciones. ¿O acaso podríamos creer, realmente, que Boca va a ganar y va a perder el mismo partido? Nota aparte, si le abrimos la puerta a la contradicción, las consecuencias son inimaginables. De hecho, el mismo Priest, célebre por sostener que algunas contradicciones son verdaderas, cree que ninguna contradicción es verdadera. Eso es contradictorio, pero a esta altura, ¿a quién le importaría?
La idea de que pensar coherentemente es deseable es un dogma que suele sostenerse sin mayor detenimiento. Sin embargo, algunos pensadores dieron argumentos a favor o en contra de esa idea. De un lado, tenemos los argumentos pragmáticos (Dutch books) y epistémicos (de adecuación) a favor de la coherencia, pero también razones para dudar del requisito de coherencia, como nos mostró la cauta profesora. Podemos decir que, si bien hay algunas respuestas bastante elaboradas a la pregunta de ‘por qué ser racionales’, se trata de un problema aún no resuelto. Uno pertinente, actual, apasionante pero, sobre todo, uno que nos permite a los filósofos entablar conversaciones sobre cómo encarar racionalmente la realidad ante una potencial victoria o no victoria futbolística.





