Respiramos, comemos, dormimos innovación. Nos asalta en carteleras de subte, discursos políticos, cursos, charlas, seminarios. Universidades, institutos, empresas y startups pelean por ser (y tal vez más todavía por ser vistos como) los más innovadores de su sector. La innovación parece ser una fuerza fundamental en el mundo en el que vivimos, pero ¿puede ser todavía más que eso? ¿Puede innovar trascender la mano humana, el acto creativo, y ser entendida como una verdadera ley de la naturaleza, una tan profunda que se funde con las de la termodinámica?
Hashtag Innovación
Si bien el proceso de innovación es parte inescapable de lo que somos, parece que venimos prestándole incremental atención en los últimos 100 años.
Frecuencia del uso de la palabra ‘innovación’ en textos publicados en inglés en los últimos dos siglos.
El desafío de comprender (o incluso definir) lo que significa innovar es tan amplio y antiguo que ha incluido esfuerzos de investigadores de las más diversas áreas, desde antropólogos o biólogas evolutivas a economistas, ingenieros o estadísticas. La primera parte de ese desafío es definir exactamente de qué hablamos cuando hablamos de innovación. ¿Es que nos referimos a una construcción técnica-mecánica como el motor a vapor, a una pieza de software, a una proteína nunca antes presente en la historia de la vida, a una canción o a una entrada de Wikipedia? ¿Necesitamos elegir un caso particular o podemos querer todavía más? ¿Podemos perseguir un objetivo ideal que sea no sólo entender el proceso de innovación en un espacio, sino entenderlo en todos?
Intentar algo así como el desarrollo de una teoría general de la innovación representaría una empresa gigantesca pero, al mismo tiempo, la cristalización de tiempos incalculables de reflexión, bosques de papel, litros de tinta y las suficientes entradas de blogs de startup para darle dos vueltas a la Tierra (aunque no necesariamente garantizando un retorno de inversión interesante).

-Acá pueden ver como usé ‘retorno de inversión’ como un chiste sobre startups. -Pero, ¿por qué estamos todos de espaldas a la pizarra?, ¿quién dejó la bicicleta en la sala de reuniones y por qué llenamos una pizarra de papeles de colores sin rótulo? -ATENCIÓN, TENEMOS UN CÓDIGO ÁMBAR. ¡DESHÁGANSE DE ELLA!
Aun en el medio del frenesí de época que rodea la idea, creo que nos estamos asomando a un modelo que bien podría ganarse el lugar de teoría general de la innovación, o por lo menos a una de las piezas fundamentales que una teoría así requiere. Todo empieza con una idea: el Posible Adyacente.
Poder ser
Stuart Kauffmann es un biólogo teórico. Su trabajo incluye estudiar eventos como el origen de la vida, o incluso trabajar sobre ideas todavía más incómodas como tratar de entender qué significa vida y qué características debe exhibir un sistema para que lo caractericemos como vivo.
En una entrevista para Edge.org, Kauffman relata el proceso de buscar generalizaciones que describan lo que ‘estar vivo’ significa:
“He estado llevando notas de lo que yo llamo ‘agentes autónomos’. Un agente autónomo es algo que puede actuar por sí mismo en un ambiente y, en efecto, todos los organismos vivos parecen ser agentes autónomos. Normalmente, pensamos en una bacteria que nada a favor de un gradiente de glucosa para conseguir comida. Eso quiere decir que hablamos de la bacteria de modo teleológico, como si estuviese actuando por sí misma [en el inglés original dice ‘on his own behalf’, que es algo así como ‘por sí misma’, pero entendido como ‘por sus propios intereses’]. Es maravilloso que el Universo haya generado cosas que puedan actuar por sí mismas. Pero ¿cómo pasó eso? (…) A medida que pensaba en esto, noté que la bacteria no es otra cosa que un sistema físico, y empecé a preguntarme qué características son necesarias para que un sistema físico sea un agente autónomo.’’
Kauffman dice que “las cosas que actúan por sí mismas, que se reproducen y son capaces de generar por lo menos un ciclo termodinámico” son agentes autónomos, y esboza cuatro reglas generales que definen la actividad de estos agentes y la construcción de los sistemas en los que estos agentes se desarrollan: la primera sostiene que los agentes autónomos buscan jugar el juego más complejo que pueden; la segunda y tercera tienen que ver con la construcción de ecosistemas y la criticalidad auto-organizada en esos ecosistemas (dos conceptos no indispensables para el lector casual, pero que preferí incluir como punta de ovillo para que los más aventureros pudieran profundizar); y la cuarta se refiere a la idea de lo adyacente posible, a la exploración de la posibilidad inmediata. Él dice que “puede ser que las biósferas sigan expandiéndose en lo posible adyacente. Al hacerlo, aumentan la diversidad de lo que puede suceder a continuación. Las biosferas maximizan la tasa de exploración del posible adyacente. Si lo hicieran demasiado rápido, destruirían su propia organización interna. (…) Exploran el posible adyacente tan rápido como pueden salirse con la suya”.
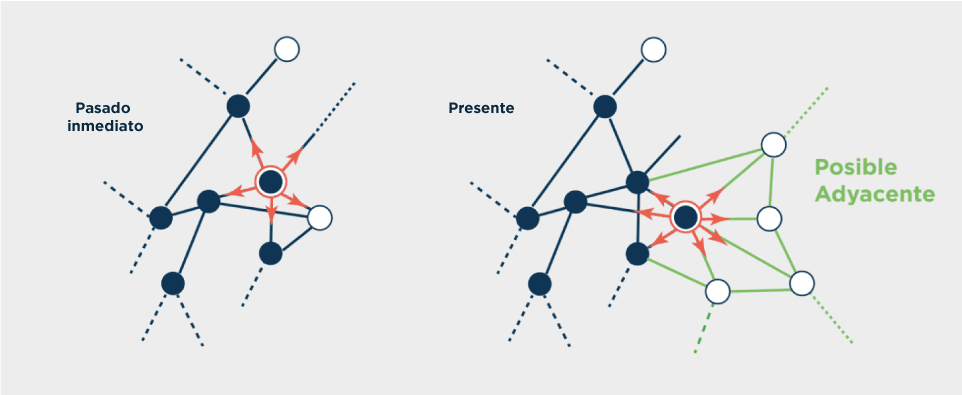
Imaginemos el presente como los puntos azules, y el futuro accesible como los puntos blancos. Apenas un punto blanco (inexplorado) se vuelve presente, el mero acto de explorarlo detona el acceso potencial a futuros nuevos, hasta el momento invisibles.
De alguna manera, Kauffman había conectado la idea de innovación y vida de una manera fundamental y, además, había presentado la noción de posible adyacente, una forma de ver la manera en la que lo vivo innova y explora posibilidades; posibilidades que no son infinitas y que están influenciadas por el pasado y por el presente. Darles un lugar central tanto a las restricciones como a la historia en el marco de cómo los organismos evolucionan, lejos de contradecir la evolución por selección natural, la complementa (o hasta podemos aventurarnos a decir que, de alguna manera, la completa, agregando una chispa autoorganizada en lugares a los que la selección natural no llega).
Este año (2017), les preguntaron a cientos de académicos qué concepto importante sentían que no estaba lo suficientemente presente en las conversaciones. Kauffman respondió ‘No ergódico’, lo que hubiera respondido cualquier persona, obvio (?). La idea de ergodicidad está muy presente en la mecánica estadística y dice que, dado un tiempo prolongado, todos los microestados accesibles de un sistema son igualmente probables. Así, los sistemas ergódicos no tienen un sentido de ‘historia’, sino que son una foto del todo.
La evolución de la vida en la Tierra, por ejemplo, es profundamente no ergódica, “El Universo no creará todas las formas posibles de vida. Esto, en conjunto con la heredabilidad de las variaciones, crea una base sustancial para (las ideas de) Darwin. La no ergodicidad nos da historia”. En los albores de la vida en la Tierra, el posible adyacente eran todas las diferentes reacciones moleculares directamente accesibles por la combinación de las moléculas existentes. Perros, piojos y girasoles estaban todavía muy distantes del posible adyacente y no fueron accesibles sino hasta mucho después en la historia de la vida.
Pensar esa historia como la exploración de determinados espacios (y no exploración de otros) así como el hecho de que cada espacio efectivamente explorado abre la posibilidad de exploración de espacios nuevos en una secuencia que va escribiendo una historia (y no otra), es una idea tan potente que rápidamente saltó de dominio.
Vivo, como una idea
En un ensayo para el Wall Street Journal que bien sirve como resumen para la tesis principal de Where Good Ideas Come from: The Natural History of Innovation, Steven Johnson tomó la idea de posibles adyacentes y la extendió a la forma en la que nacen las ideas nuevas. Para él, “el posible adyacente es una especie de sombra del futuro que se cierne sobre los bordes del estado actual de las cosas, un mapa de todas las formas en las que el presente puede reinventarse”. Una anécdota absolutamente tribunera, pero no por ello poco pertinente, cuenta que Stephen Jay Gould tenía una colección de sandalias hechas de neumáticos reciclados y que él mismo rescataba de esa costumbre una debilidad por la metáfora sobre la evolución por selección natural (la respuesta a ‘¿está chequeado ese dato?’ es sí). La innovación en el mundo natural depende, de la misma manera que los pies de Gould, de trabajar sobre piezas recicladas. En la misma línea, el biólogo (y premio Nobel) François Jacob definía la evolución no como la acción de una ingeniera, sino más bien la de un bricoleur. Y sí, suena como bricolage precisamente porque se refiere a aquel que arma y desarma, que juega con lo que tiene. La naturaleza ata con alambre, digamos.
Johnson discute en su libro muchos eventos distintos de invención (desde motores hasta máquinas de calcular, pasando por la creación de YouTube), pero se detiene particularmente en un ejemplo claro y contundente: la imprenta de Gutenberg.
Cerca de 1440, Johannes Gutenberg venía de fracasar estrepitosamente vendiendo espejos pequeños que les permitían a los peregrinos ver las reliquias durante las procesiones (y que, supuestamente, les permitían así capturar los poderes mágicos de las reliquias). Pésimo timing de mercado para Johannes haber convivido con una peste bubónica que adelgazó las filas de los fieles (aun los protegidos por los espejos captadores de poderes). Como no hay epidemia diezmadora de poblaciones que por bien no venga (?), Gutenberg hizo lo que sus colegas contemporáneos hashtag emprendedores definen como pivotear.

Anunciaste mal el Oscar a Mejor Película. Prefiero verlo como que pivoteé el Oscar a Mejor Película.
Gutenberg se había familiarizado con la tecnología vitivinícola de la época, pero no estaba interesado en el vino sino en una de las tecnologías del vino: la prensa. Los caracteres móviles ya habían sido inventados e implementados de manera independiente por un herrero chino siglos atrás, pero al ser aplicados manualmente no habían logrado escalar como tecnología significativamente distinta de la escritura a mano. Gutenberg no tenía ningún entrenamiento en hacer vino, pero sí sabía de metalúrgica; si a eso le agregamos que desarrolló un prototipo de tinta al aceite que es el antecesor común de muchas de las tintas hoy usadas, podemos ver un bricoleur que dispone de todos los elementos necesarios para la imprenta. Johannes había tomado múltiples elementos disponibles (algunos provenientes de industrias muy lejanas entre sí) y había imaginado un posible adyacente que los remixaba a todos, generando algo que era mucho más que la suma de las partes y que cumplía con una de las características más importantes de la innovación: abría la puerta a nuevos espacios. Pateaba hacia adelante la frontera de lo posible lo suficientemente lejos como para ser novedoso, pero también lo suficientemente cerca para que los demás lo pudieran seguir.
El posible adyacente es entonces esa frontera en expansión; es el conjunto de todas las ideas, palabras, canciones, moléculas, genomas o tecnologías posibles que están a un paso de lo que existe. La creación de algo en particular que colapsa el espacio de posibilidades inmediatas explorables en una efectivamente explorada, es lo que a su vez genera un espacio nuevo de posibilidades potenciales.
Abrir la caja para ver cómo está el gato es lo que nos genera la nueva adyacencia de enterrarlo en el jardín o hacerle un mimo.
Formalicemos
Hablar de espacios, de novedad o de posibles adyacentes es interesante. La narrativa es amplia y seductora por su capacidad transversal, pero formalizarla nos permite, entre otras cosas, minimizar las interpretaciones y, en el mejor de los casos, indicarnos puntos ciegos sobre la propia teoría o perseguir la aventura de intentar observaciones de nuestro entorno (e incluso predecir el ritmo de aparición de innovaciones futuras).

Un modelo general de invención que capture la idea de posibles adyacentes debería, por lo menos, cumplir dos condiciones generales: predecir correctamente eventos observables, como por ejemplo el ritmo al cual las novedades aparecen y la forma (estrictamente, la frecuencia) en la que se exploran las regiones conocidas del espacio; e incluir la idea de que la aparición de una novedad (la exploración puntual de un posible adyacente) genera la aparición de nuevos espacios plagados de novedades hasta el momento desconocidas (o no accesibles dado que se encontraban por fuera de los posibles adyacentes). Con esto no estaríamos todavía para cenar en la embajada, pero tenemos una idea que acaba de abandonar el short de entrenar y la remera agujereada por algo que bien podría pasar desapercibida en la fila del banco.
Ritmo y sustancia
A veces nos topamos con descripciones de la realidad que no tenemos idea de dónde vienen, pero que funcionan, y funcionan tan bien que se ven representadas en múltiples dominios que a priori no imaginamos como evidentemente análogos. Uno de esos modelos es la Ley de Heaps, que describe la forma en la que aumenta el tamaño del vocabulario (la cantidad de palabras únicas observadas en el texto) en función de la cantidad de texto que se observa.
En particular, postula que el tamaño del vocabulario es una función del tamaño del texto de esta forma:

Donde Vr es la cantidad de palabras únicas, n es el tamaño del documento y K y β son constantes que dependen del texto (es decir, son particulares para cada texto) y del idioma (para el inglés, por ejemplo, K es entre 10 y 100, y β entre 0,4 y 0,6).
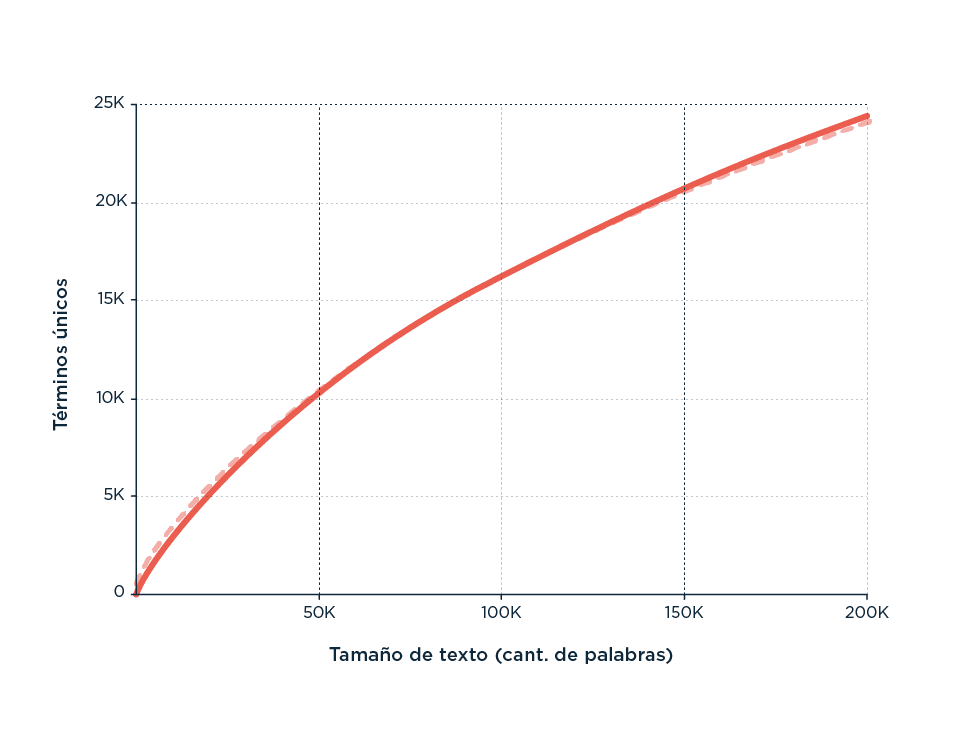
Curva típica de Heaps para el análisis de texto en inglés (como fuente se usaron artículos de diario).
Pero la Ley de Heaps se pone más general cuando se empieza a observar que no sólo describe la aparición de palabras nuevas en corpus de texto, sino también la aparición de genes nuevos a medida que secuenciás genomas completos.
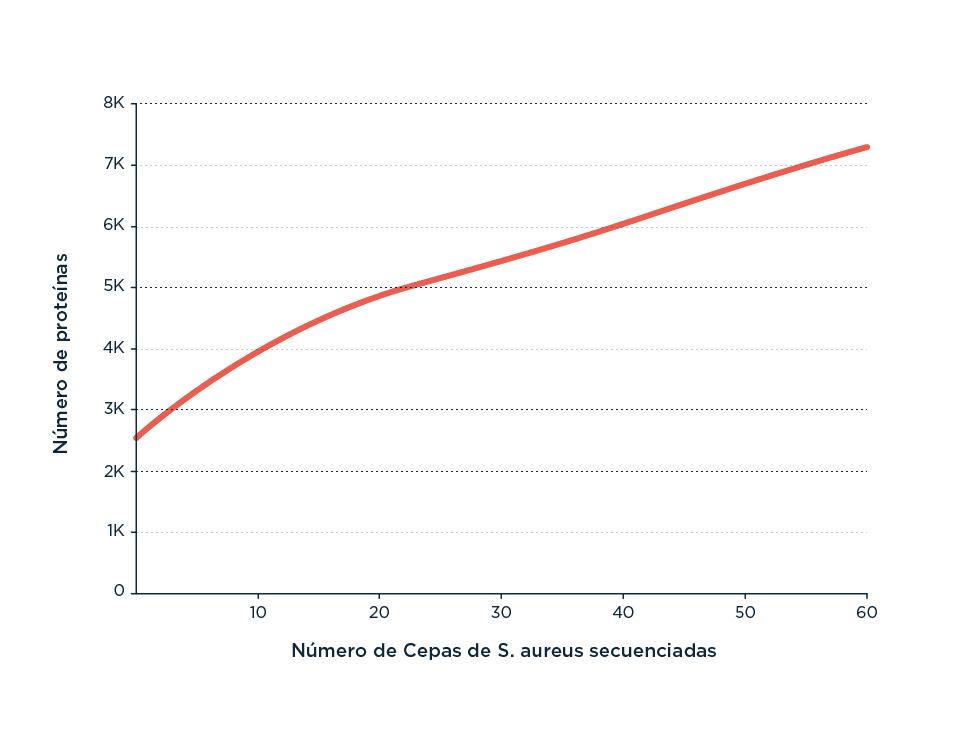
Aparición de una curva típica de Heaps para el análisis de la frecuencia de aparición de genes nuevos a medida que se van incorporando al análisis genomas completos (Fuente).
Entonces, una descripción formal de un modelo que contenga la idea de posibles adyacentes como descripción del proceso de innovación debería, de alguna manera, predecir la aparición de un patrón observable en la incorporación de lo novedoso a medida que se explora lo desconocido como es la Ley de Heaps.
Lo que es, es
La segunda condición para poder formalizar la idea de posibles adyacentes es mapear lo posible y entender cuánto accedemos a cada parte de ese territorio. Afortunadamente, hace muchos años que nos tropezamos con otra ley empírica, otro patrón que aparece una y otra y otra vez: la Ley de Zipf.
Nombrada así por George Kinglsey Zipf, un lingüista de principios de siglo pasado que notó una regularidad interesante en la forma en la que se relacionan la frecuencia de uso de las palabras y el ranking de uso (aunque, estrictamente, el mismo Zipf reconocía que la idea lo precedía, aparentemente de la mano de un estenógrafo francés). Esta relación aparecía cada vez que analizaba un corpus de texto, siendo el ejemplo paradigmático el Brown Corpus (una colección de textos de cerca de un millón de palabras de orígenes varios que buscaba representar el idioma inglés americano). En él, la palabra ‘the’ aparece como la más frecuente, con 69.971 ocurrencias (algo del 7%), seguida de la palabra ‘of’ con 36.411 ocurrencias (3,5%), y después ‘and’, con 28.852 (2,9%). El patrón empieza a vislumbrarse cuando ves que la frecuencia de aparición de cada palabra es aproximadamente proporcional a 1/(su posición en el ranking de ocurrencia). Entonces, la segunda va a aparecer aproximadamente ½ que la primera, la tercera aproximadamente ⅓ que la primera y así, en una forma general que puede expresarse como:

Donde Pn representa la frecuencia de la n-ésima palabra más frecuente y el exponente a es un número real positivo, en general ligeramente superior a 1 (en inglés, por ejemplo, el exponente es cercano a 1,07, y por eso funcionó tan bien para identificar ‘a ojo’ el patrón por primera vez). En este punto es interesante decir que una ley no empírica, pero más precisa, derivada de los trabajos de Claude Shannon, fue descubierta por Benoît Mandelbrot, cosa que, lejos de desviarnos del tema central, nos pone de frente a él: qué pasa cuando lo observacional, lo (¿aparentemente?) fundamental y que no deviene de la observación empírica sino de aproximaciones teóricas, se tocan.
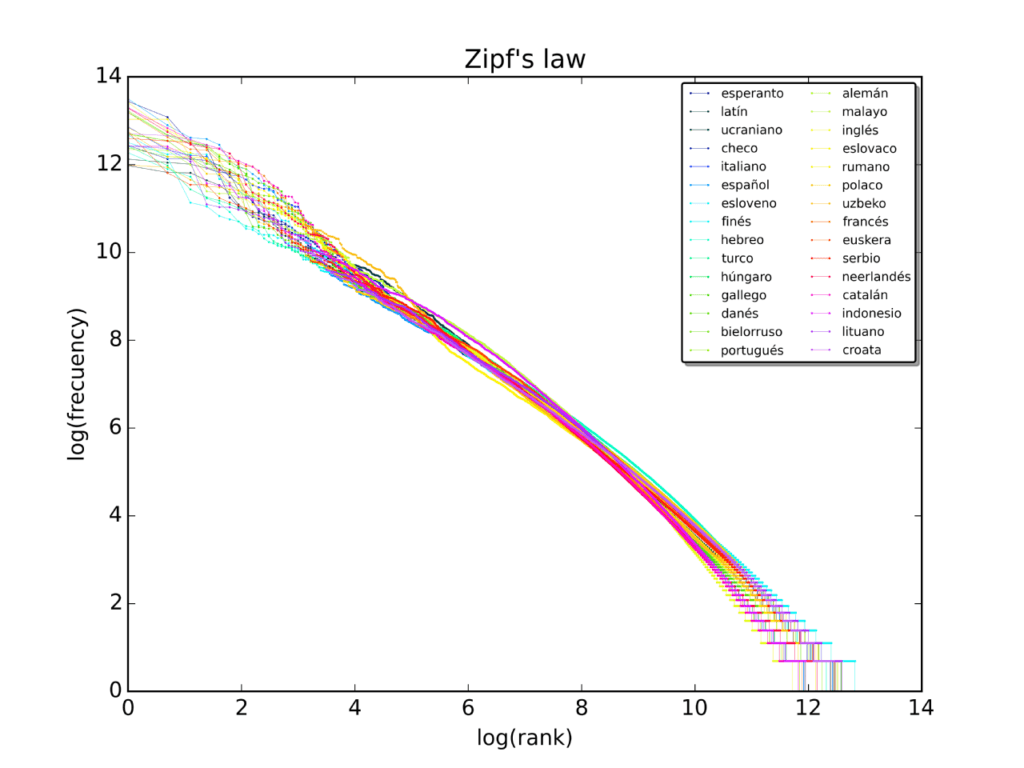
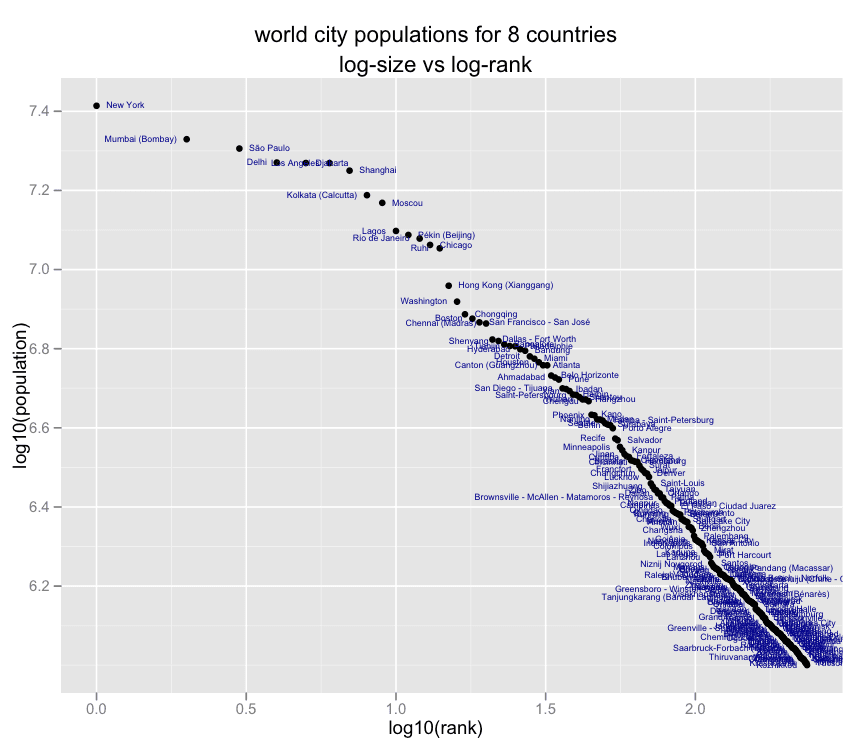
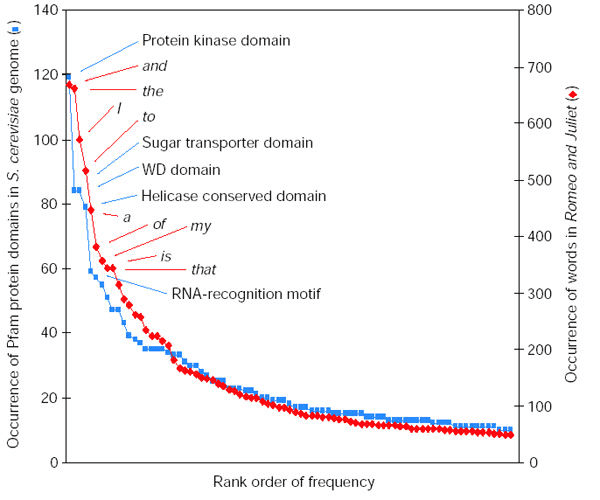
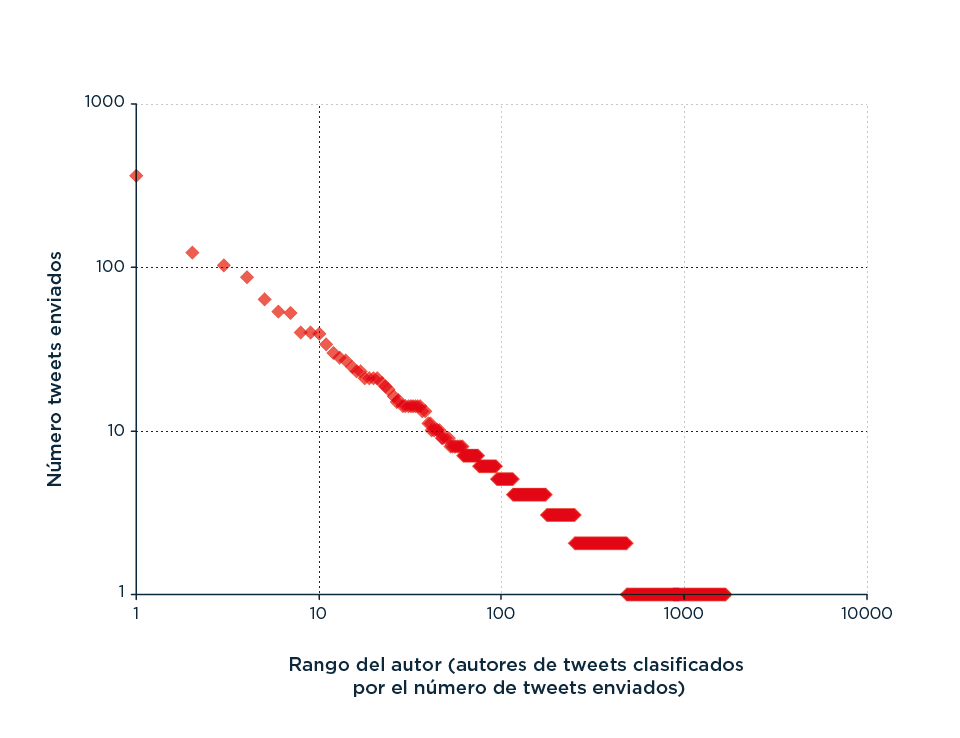
La Ley de Zipf parece ser uno de esos patrones que, una vez visto, no puede dejar de encontrarse una y otra y otra vez, al punto que muchos tipos de datos distintos pueden ser aproximados a una distribución tipo Zipf, desde datos que vienen de la distribución de las palabras en corpus de texto hasta distribuciones de frecuencia como la cantidad de habitantes en las ciudades, la presencia de distintos dominios en proteínas en un genoma, la cantidad de tráfico en los sitios de internet, el número de citas en papers y hasta el número de tuits sobre un determinado paper.
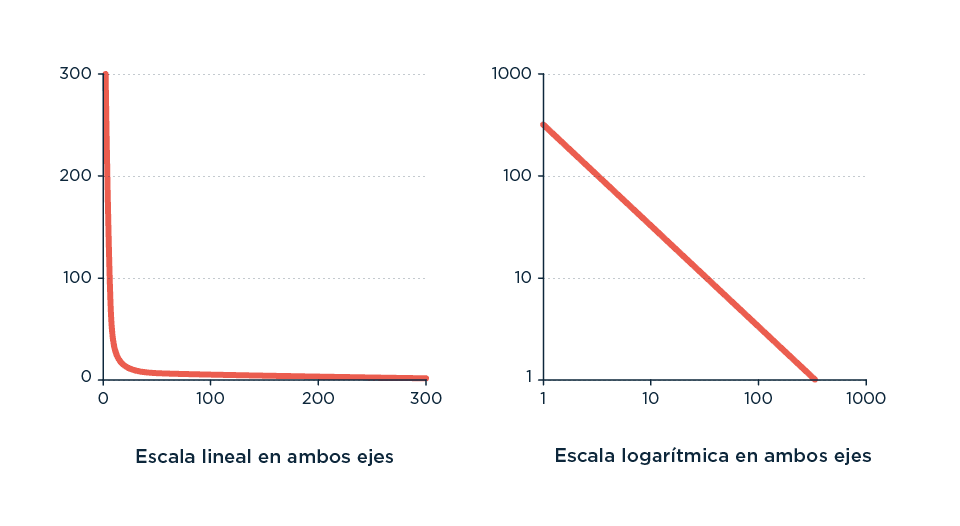
Figura CLAVE para el grupo que intersecta los no amantes de graficar cosas con los no amantes de los logaritmos. Dado que las distribuciones tipo ‘power-law’ son relaciones exponenciales, una forma de observar más claramente los patrones es graficar los puntos no en un eje lineal sino en un eje donde tanto la x como la y son transformadas aplicando el logaritmo. Así, pasamos de la interesante pero difícilmente informativa forma de L en el gráfico lineal-lineal a la coqueta linealidad del gráfico log-log. Esta es la razón por la que algunas de las figuras que representan distribuciones de Zipf lucen de una manera y otras de otra, aun siendo solamente dos formas visuales de representar lo mismo. Lo importante acá es tatuarse ‘atención: leer siempre los ejes’.
Estas distribuciones tipo Zipf (el término en inglés es Zipfian, pero siento que usar Zipfiano en este texto me priva de usarlo como nombre para mi civilización intergaláctica regida por leyes basadas en la matemática en la novela que jamás voy a escribir), están relacionadas con (o son una forma particular de) las distribuciones de tipo power-law, o sea, toda distribución donde una magnitud está relacionada con una potencia. La más familiar de esas distribuciones aparece en la Ley de Pareto, también llamada 80-20, donde el 80% de la frecuencia de una ocurrencia es explicada por el 20% de las ocurrencias (y visceversa).
Llegado este punto, viendo Zipf por todos lados y tratando de entender si era real o pareidolia, me pregunté si tenía algún dataset para ajustar, de esos que debería ajustarse a una distribución tipo Zipf, así que me pareció divertido ponerme recursivo y mirar, precisamente, dos promesas Zipf: 1) Si sos tan ubicua como prometés, el tráfico del Gato del último año debería ajustar a una distribución tipo Zipf. 2) Si te la bancás todavía más, mi querida distribución, la frecuencia de uso de palabras en el Gato debería, de la misma manera, ajustar a un patrón tipo Zipf.
A un Analytics de distancia sencillito, bajé el tráfico de Gato, lo grafiqué y sí pude creer lo que pasó a continuación:
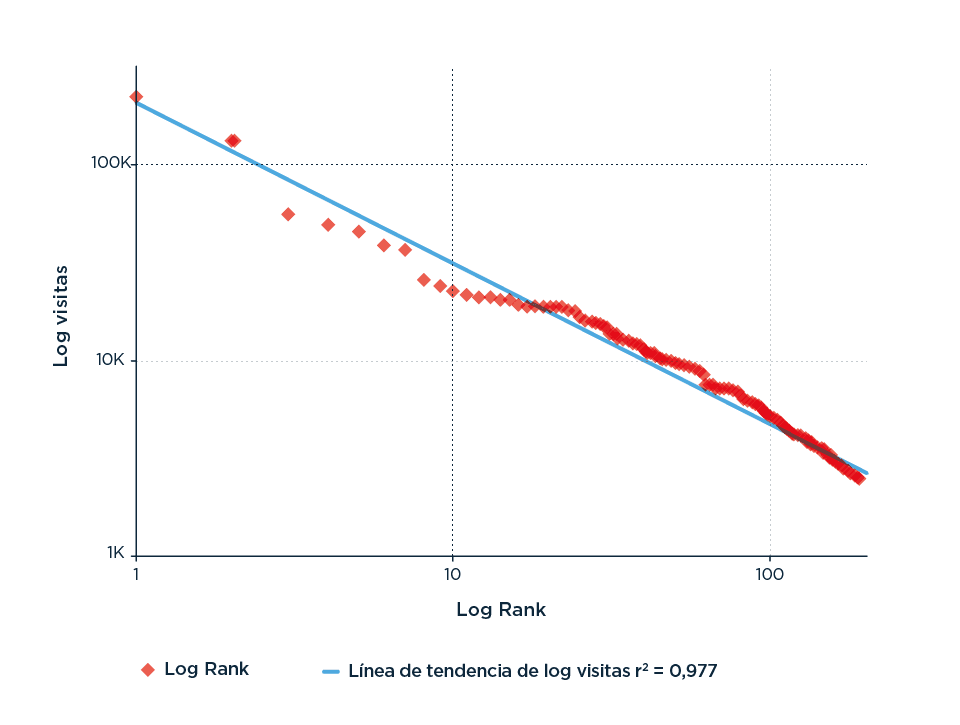
Acá podemos ver si el tráfico del Gato se ajustaría bastante bien a una distribución de tipo Zipf. En el eje x, el logaritmo de la cantidad de visitas vs el logaritmo del orden (de la página más visitada a la menos visitada).
Envalentonado yo −y contando con amigos que manejan Python (atribución indispensable de crédito a Pablo Riera en este punto)− convertimos juntos todas las notas del último año a texto y aprovechamos un script para ordenar la frecuencia de palabras en función de su ranking de uso y graficarlo (acá los txt, por si alguien quiere jugar).
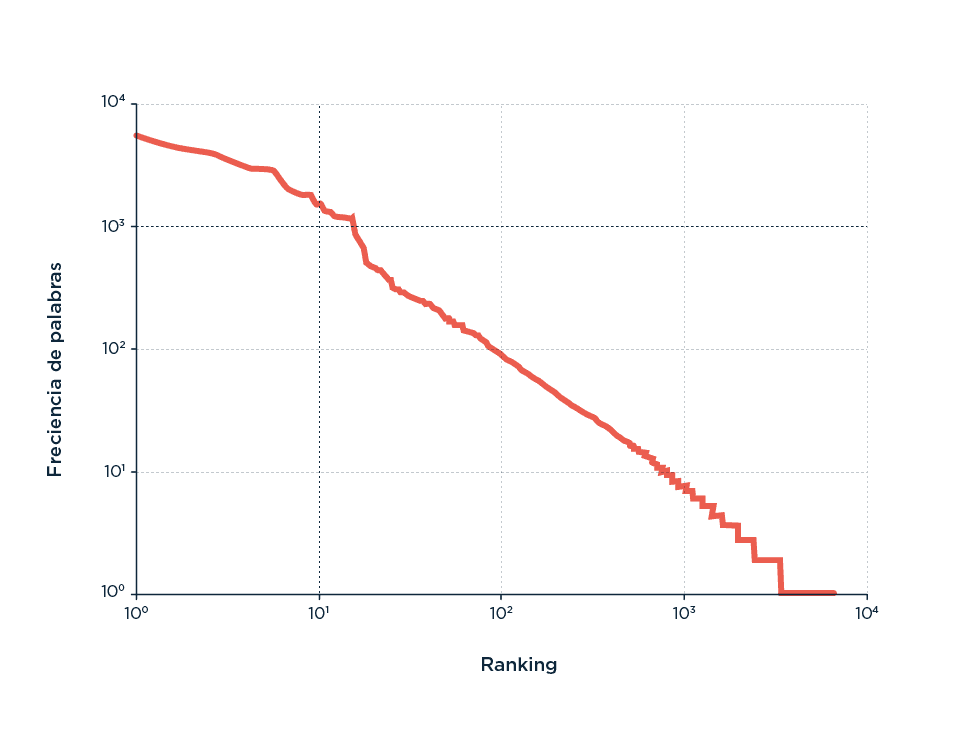
Podemos ver acá si el uso de palabras del Gato se ajusta bastante bien a una distribución de tipo Zift. En el eje x, el logaritmo de la frecuencia de uso de palabras vs. el logaritmo del orden de la palabra más usada a la menos usada.
Una y otra y otra vez aparece Zifp. Siempre que exploramos lo conocido y lo caminamos, aun en dominios que parecen no tener demasiado en común más que ser eso: exploraciones de lo conocido. Ahora, como la idea de posibles adyacentes no sólo promete explicar la novedad sino también la relación entre lo que ya existe, no debería escaparse de explicar, también, estas ocurrencias.
La misma Stacey Malibú, pero el sombrero es nuevo
‘Lo nuevo’ puede definirse de varias maneras, que incluyen tanto novedades (aquello que es nuevo para mí pero no para los demás) como innovaciones (aquello que es nuevo para todos). Esta idea ha sido abordada muchas veces desde muchos ángulos distintos, a veces abstractos y otras veces anecdóticos, pero nunca desde perspectivas más bien teóricas (o de modelos generales, si se quiere). Precisamente por eso es que, una vez que me tropecé con el trabajo de Vittorio Loreto, no pude sacudírmelo, porque intenta tomar ideas esparcidas en la literatura (científica y menos científica) y formalizarlas. La idea de Kauffman primero, y la generalización de Johnson después, habían ganado muchísima popularidad, pero popular y sólido no son lo mismo.
El primer gran desafío que describe Loreto es superar el problema intrínseco que existe en tratar de estimar las probabilidades de eventos futuros basado en datos del pasado (la paradoja de la inferencia), y para explicarlo cita a S. L. Zabel, filósofo, lo que al mismo tiempo que le soluciona tener que inventar dos veces la pólvora nos recuerda que la filosofía es absolutamente necesaria para hacer ciencia. Para Zabel, “El problema no es observar lo «imposible», es decir, un suceso cuya posibilidad hemos considerado, pero cuya probabilidad juzgamos que es 0. Más bien, el problema surge cuando observamos un suceso cuya existencia ni siquiera sospechamos previamente; este es el llamado problema del ‘conocimiento imprevisto’”.
Loreto encuentra en el modelo de posible adyacente la oportunidad de resolver esta imprevisibilidad, por lo menos acotándola a los márgenes inmediatos del presente. A la frontera entre lo existente y lo posible: “La definición de posible codifica en sí misma la dicotomía entre lo real y lo posible: la concreción en la realización de un fenómeno dado y el espacio de posibilidades todavía inexploradas”.
Ok, Vittorio, tenés mi atención. Ahora necesito que me muestres que tu formalización del modelo de posibles adyacentes cumple por lo menos con las 3 condiciones que debería:
Condición 1: El modelo de posibles adyacentes tiene que predecir la Ley de Heaps.
Condición 2: El modelo de posibles adyacentes tiene que predecir la Ley de Zipf.
Condición 3: El modelo de posibles adyacentes tiene que predecir la forma en la que una novedad permite el acceso a novedades subsiguientes.
Talk the talk, walk the walk
Qué inconsistente (por no decir qué tiro en el pie) sería que Loreto dijese ‘bueno, este modelo que trata de formalizar matemáticamente la idea de posibles adyacentes se me ocurrió de la nada y no se apoya de ninguna manera en conocimiento previo’. Pero no. Leer su trabajo es leer también la historia de cómo, a través de recombinaciones de ideas existentes, su grupo llega a concretar esta idea. Qué lindo, qué recursivo, qué consistente todo, Vittorio.
El punto más proximal sobre el que construye es la idea de una Urna de Pólya: un tipo de modelo estadístico muy útil para describir situaciones del tipo ‘Una vasija contiene ‘x’ número de bolitas blancas e ‘y’ número de bolitas negras. Cada vez que meto la mano y saco una, la observo y devuelvo a la vasija no sólo la que agarré, sino otra del mismo color’, que se usa para modelar la cantidad de bolitas de cada color a medida que el tiempo progresa, y que, dada su capacidad de autoregularse positivamente, a veces es descrito como un modelo donde ‘los ricos se hacen más ricos’. El elemento clave en el que este modelo se hace útil al describir la idea de posibles adyacentes es cómo cada evento determina la posibilidad de ocurrencia de un evento futuro. Cómo se captura la forma en la que la frecuencia de lo actual (las pelotitas en la vasija) repercute sobre los eventos futuros (al devolver bolitas basado en qué se sacó, las probabilidades futuras están directamente afectadas por el pasado).
Este modelo así como está describe muy bien la evolución de frecuencias en el tiempo, pero esas frecuencias siempre tienen que ver con lo existente, no hay un parámetro de innovación. Hay bolitas blancas y bolitas negras, y son siempre esas las opciones.
Pero ¿qué pasa si combinás una Urna de Pólya con la idea de posibles adyacentes? Aparece un modelo que está pegado a los dos, en la frontera de lo posible: el modelo de Urna de Pólya con gatillo por la novedad. ¿Qué quiere decir esto?
Imaginemos una nueva urna llena de pelotitas de colores (vamos a bautizarla U basados en una falta total de creatividad). Ahora, imaginemos que anotamos cada vez que sacamos una pelotita de color en una lista, y llamamos a esa secuencia de anotaciones S. Acto seguido, metemos la mano en U y sacamos una pelotita. La pelotita es roja. Miramos la lista S que nos cuenta la historia de todas las que sacamos antes, y vemos que no hay ninguna roja. Como esto constituye una novedad, agregamos a la urna algunas pelotitas rojas (como antes agregábamos blancas al sacar una blanca), pero también metemos la mano en una urna opaca y agregamos un puñado de pelotitas de colores nuevos, distintos, que no conocemos.
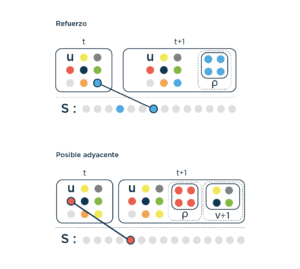
Acabamos de incluir novedades de las que sólo sabemos eso (que no estaban presentes antes), pero sin saber exactamente qué son, conservando así al mismo tiempo la idea de novedad y un velo de ignorancia sobre qué novedad.
La Urna de Polya con gatillo por la novedad es, entonces, un modelo que incorpora las frecuencias de lo existente (Zipf), la aparición de lo nuevo (Heap) y en el que cada novedad detona la inclusión de nuevas novedades. Un avance significativo hacia una teoría general de la innovación.

O sea que funciona. O, para ser estrictos, este es el momento en el que un modelo se encuentra en uno de sus puntos más interesantes: en teoría funciona. La pregunta es si además de funcionar en modelos teóricos, también es capaz de emular las situaciones observables en condiciones naturales (empezando por reproducir la aparición de curvas tipo Zipf y tipo Heaps). Y sí.
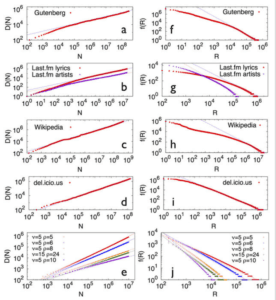
Podemos ver en a-d y f-i datos reales de Wikipedia, Last.fm, del.ici.ous y el Proyecto Gutemberg reproduciendo las leyes de Zipf y Heaps. e y j muestran lo que pasa cuando se pone a correr el modelo de Urna de Polya gatillada por novedad, y se generan modelos que reproducen ambas leyes. El trabajo original también incluye modelados muy interesantes sobre la entropía de los datasets (tanto la entropía local como global), y cómo este modelo reproduce fenómenos observados en estos datasets, lo que le da mucha robustez a esta idea pero es un poco más árido de compartir y prefiero dejarlo para los aventurados).
Parece que sí, que cuando se hacía correr este modelo simulando situaciones iniciales diferentes (números distintos de pelotitas iniciales y formas distintas de reaccionar a cuántas o cuáles agregar), todas las condiciones que definimos antes como necesarias aparecían: 1) la frecuencia en la que se exploraba lo conocido, 2) la forma en la que aparecia lo novedoso y 3) cómo lo novedoso generaba novedad. Así, tenemos un modelo que además de ser elegante, bello de observar y relativamente simple, se ajusta a la observación empírica.
I’m so Meta, Even This Acronym
Me encantan las ideas. Las grandes, las chicas, las buenas, algunas divertidas, inclusive algunas tan extraordinariamente malas que se vuelven experiencias estéticas.

Roberto, ¿esto es prudente?
Vos pensalo como una experiencia estética.
De todas las ideas, las que más me gustan son las que me permiten acomodar otras. Darles forma dentro de un marco que hace que pueda asirme de ellas mejor para poder meterles mejor las manos. La teoría atómica, la ley de grandes números, los juegos de no suma cero o la evolución por selección natural son ideas acomodadoras de ideas. Posibles adyacentes también, y parece llegar en un momento donde el énfasis en la innovación como proceso se impone en las vidas de todos. Una idea primero difusa que, aun en su imprecisión, conquista la atención de personas de distintos ámbitos que la usan para acomodar sus demás ideas. Para ver a través de ella procesos, para generar narrativas de largo arco que hilan desde el principio de la vida hasta la llegada de YouTube. Esta es una idea sobre las ideas que recorre el camino completo, hasta constituirse en una enunciación formal lo suficientemente bien definida para ser puesta a prueba, ganar así de a poco espalda, y al mismo tiempo darse el gusto de poder contar su propia historia de la que es protagonista y narradora. Mordiéndose la cola al llegar, explicándose a sí misma, conteniendo su pasado y mostrándonos la sombra de un futuro del que no podemos saber mucho más que el hecho de que la única forma de acceder a él es juntando pedazos de presente e inventándolo.





