Llegó el momento de enfrentarse a una verdad que va a cambiar la forma de comportarnos en presencia de banditas elásticas. Yo me deformo, tú te deformas, el Universo se deforma, nosotros nos deformamos. Todo se deforma porque deformarse es mucho más cotidiano de lo que imaginamos. Pero ¿qué es la deformación?
Hablando desde lo muy general y pensando en cualquier cosa u objeto habitual, lo que sabemos es que, si hacemos poca fuerza sobre algo, se deforma poco; si hacemos mucha fuerza, se deforma mucho; y si hacemos mucha mucha fuerza, destruimos ese algo. Pero el tema es un poquito más profundo: no siempre es sólo fuerza lo que deforma. Las deformaciones son la consecuencia de entregarle energía a algún elemento (cosa, objeto, persona, etc). En la gran mayoría de los casos, esa energía aparece disfrazada de fuerza o presión (que es fuerza por unidad de superficie), pero también puede ser energía en otras formas, como el calor que hace que en invierno las puertas cierren mejor que en verano.
NdE: esta nota probablemente haya roto el récord de conjugaciones de ‘deformar’. Que se sepa que fue a mi pesar. O quizá no sea tan grave y esta aclaración en realidad sólo se trate de una deformación profesional.
Los materiales, a nivel micro y macro, se deforman más o menos dependiendo de cuánto absorban la energía que se les entrega. Básicamente, si aguanta todo lo que recibe, se deforma; si no, se rompe. Por eso decimos que las deformaciones son ese margen que viene a aliviar un poco la vida de quienes tenemos tendencia a romper cosas (o, en términos más académicos, los torpes).
¿Cómo funciona esto? Las cosas están hechas de algún material; ese material, de moléculas; esas moléculas, de átomos. Los átomos están unidos entre sí por estructuras que, simplificando mucho, podríamos decir que son como resortes: si lo aprieto, se achica; si lo estiro, se agranda.
Un señor llamado Robert Hooke pensó en esto allá por el 1676. Mientras se peleaba con media comunidad científica de la época y reclamaba crédito por los descubrimientos de la otra mitad, jugaba con resortes. El tipo vio que si se aplica una unidad de fuerza a un resorte, éste se alarga o se encorva por una unidad de espacio, mientras que si se le aplican dos unidades de fuerza, el resorte se alargará o encorvará dos unidades de espacio; tres lo alargarán o encorvarán tres, y así sucesivamente. Es decir que la fuerza del resorte es proporcional a la deformación del mismo. En este caso, la fuerza del resorte es igual a la del peso (carga) aplicado al mismo, y ambas fuerzas deben ser iguales para que el sistema esté en equilibrio (en este caso, para que deje de estirarse o contraerse el resorte).

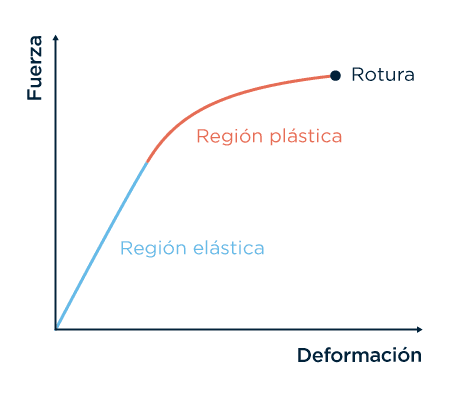
Este comportamiento proporcional vale dentro de un rango llamado ‘región elástica’, en el que las deformaciones no son permanentes una vez retirada la carga (la fuerza). Si graficamos esta relación entre deformación y fuerza, vamos a ver una recta.
Pero cuando Hooke aplicaba mucha fuerza, notaba que los resortes se deformaban más de lo que indicaba esta recta (es decir, se perdía esa relación proporcional entre fuerza y deformación del resorte). De hecho, con cada unidad de fuerza adicional, se deformaban más que con la anterior. Este rango ya no lineal se conoce como ‘región plástica’.
Que la fuerza y la deformación te acompañen.
Hooke veía que, en la región elástica, los resortes recobraban su forma original cuando se les quitaba la fuerza (lo llamó ‘comportamiento elástico’). Pero en la región plástica, los resortes ya no recuperaban completamente su forma original cuando se sacaba esa fuerza, quedando deformados (a esto le puso ‘comportamiento plástico’). Finalmente, si seguía aumentando la fuerza y se pasaba de la región plástica, el resorte se rompía.
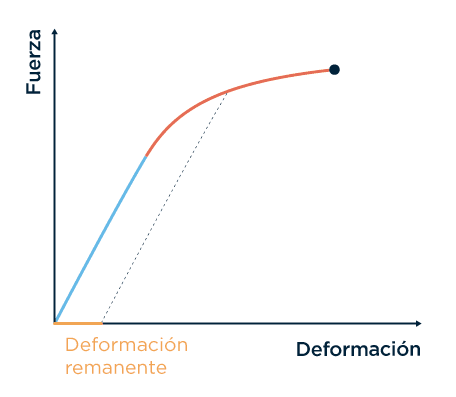
Lo que él en su época aún no conocía pero hoy sí sabemos es lo que hace que, en el régimen plástico, el material no recobre su forma original y quede deformado cuando se retira la carga, y es que los enlaces entre átomos, moléculas o cristales, no logran restablecer la condición previa a la deformación. Al quitarle la fuerza le queda una deformación remanente y el material busca su forma original sin alcanzarla, pasando por una recta paralela a la del comportamiento elástico.
Ya no sos igual.
Y fue así como, algún miércoles de 1678, probablemente armado de un brutal juego de pantuflas, una taza de café en su mano y una pluma de pájaro entintada, Robert Hooke entraba por la puerta grande de la resistencia de materiales. Mientras estaba hasta las manos seguramente no haciendo algo que Robert Boyle le había encargado (Hooke era su ayudante), se puso a escribir lo que observó en sus años de jugar con pesas y resortes y lo publicó en un trabajo llamado De potentia restitutiva. Este trabajo contiene la famosa afirmación (expuesta a la comunidad científica en forma de anagrama como: ceiiinosssttuv; un buena onda): “ut tensio sic vis”. Traducido, es algo del estilo de ‘como la tensión, así la fuerza’. Para los que no sabemos latín, a esto lo conocemos como la Ley de Hooke.
El límite que separa la región elástica de la plástica es la fuerza a partir de la cual el material no logra volver a su forma original, conocida como ‘límite de elasticidad’; mientras que el límite superior de la región plástica, es decir la fuerza a la cual el material se rompe, es el ‘límite de rotura’. Estos límites no son precisos. De hecho, hay límites de elasticidad y de rotura para diferentes esfuerzos (tracción, flexión, torsión, etc), diferentes temperaturas, y algunas otras variables. Eso sí, todos los límites dependen fundamentalmente del material, lo que hace que encontrarlos requiera muchos ensayos y estadística.

“Muchos ensayos y estadística”.
Esto lo vivimos a diario, por ejemplo, cuando sacamos nuestro niño interior y nos ponemos a jugar con una bandita elástica. Primero la estiramos un poco y vuelve a como estaba antes, o sea que hasta ahí tuvo, haciendo honor a su nombre, un comportamiento elástico. Después, alterando la entropía del Universo y desafiando el azar, la estiramos un poco más para ver que, cuando la soltamos, ahora queda estirada. Ahí es cuando pasamos el límite elástico y el material entró en la zona de comportamiento plástico. Después, ya subversivos, la estiramos todavía un poco más, superamos el límite de rotura del material y la bandita nos devuelve toda la energía que tenía almacenada directamente a nuestro dedo.
En resumen, un material que tenga un comportamiento elástico perfecto almacena toda la energía que se le entrega y luego la devuelve cuando ya no se aplica la fuerza. En la otra esquina, un material de comportamiento plástico perfecto absorbe toda la energía entregada: una parte la disipa (en forma de calor, por ejemplo), y otra parte la utiliza para deformarse. Ojo, esto funciona sólo para materiales perfectos. No existe tal cosa en la vida, pero hay materiales que se acercan bastante a estos extremos.
Ahora ¿qué pasa con las cosas que se rompen de una, como la pantalla de un celular después de batirse a duelo (y perder) contra la vereda? Cada material tiene propiedades que definen básicamente qué cantidad de energía puede absorber antes de romperse. Esto significa que la difunta pantalla del dispositivo de comunicación sí se deformó absorbiendo algo de energía, pero superó el límite de rotura y chau celu. Los materiales frágiles tienen la particularidad de alcanzar el límite de rotura con muy pocas deformaciones. Esto quiere decir que podemos venir deformando algo como unos campeones (región elástica) hasta que de repente, sin aviso ni mucha deformación mediante, se rompe. En estos materiales, la región plástica es muy corta y a veces hasta inexistente.
Un material como el hormigón por ejemplo, de nombre rudo y tan popular en la construcción, es de hecho relativamente frágil. Hace falta agregarle barras de acero, fibras o alguna otra cosa dúctil para que sea más seguro. Y seguro quiere decir, aunque suene un poco anti intuitivo, que sea capaz de deformarse. No es lo mismo ver que tu casa se empieza a deformar lentamente, lo que te da tiempo a salir corriendo, a estar tomando mate tranquilo y que de golpe te me desplome encima.

Deformate que me gusta (y me salva): el Tacoma Narrows Bridge es un ejemplo claro de que las deformaciones otorgan seguridad a las estructuras, permitiendo a la gente que las usa anticipar un eventual colapso.
Ahora, dado que todo esto de las deformaciones parece ser tan fundamental, debería existir alguna manera de describir este asunto de una forma más universal, como para poder hacer numeritos y ver cuánto se deforman las cosas. Y por suerte la hay. Como dijo Hooke, la deformación es proporcional a la fuerza. A esto se lo llamó módulo de elasticidad o módulo de Young (otro inglés de pantuflas): es una relación entre fuerza y deformación que depende del material y, como dijimos, es constante sólo en la región elástica y lineal. En otras palabras, nos dice cuál es la pendiente de la recta en la región elástica. A menor módulo de elasticidad (E), la recta es más horizontal y logramos mucha deformación con poca fuerza; a mayor módulo de elasticidad, para mucha fuerza hay poca deformación. Las divertidas y traicioneras banditas elásticas tienen bajo módulo de elasticidad, lo cual hace que con poca fuerza se estiren mucho.
Matemáticamente, la Ley de Hooke (para el caso de resortes) tiene esta forma:
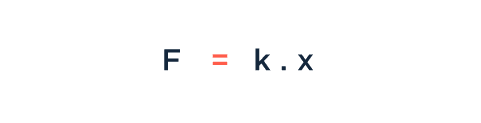
En donde F es la fuerza aplicada, k es la constante del resorte (asimilable al módulo de elasticidad E) y x es lo que se estira o acorta el resorte. Generalizando esa misma ecuación, queda:

En donde F/A es una tensión (es decir que al dividir por el área hago que distintas fuerzas en distintas secciones sean comparables), A es el área transversal a la fuerza aplicada, E es el módulo de Young, ∆L es el alargamiento respecto de la longitud inicial, y L es justamente la longitud inicial.
Esto quiere decir que al aplicar una fuerza F, el resorte se estira o se alarga k veces una distancia x. Si la fuerza es igual a cero, se alarga cero. Si la fuerza tiene un valor distinto de cero, podemos despejar cuánto es el valor de la famosa x y eso sería la distancia que se estiró o alargó el resorte. Esto está llevado a resortes por simplicidad en el desarrollo matemático de la cuestión, pero claramente es extrapolable (a partir de ecuaciones parecidas) a objetos, materiales y muchas otras cosas más interesantes (sin ánimo de ofender a ningún fanático de los resortes).
Algo curioso es que hasta 1807, cuando Thomas Young ‘descubrió’ o ‘definió’ el módulo de elasticidad, la Ley de Hooke no era más que una linda e intrigante frase tirada al aire, casi sin aplicación práctica, aunque se intuía que todo funcionaba un poco de esta manera. Pero bueno, lo divertido siempre está en plantear algo y demostrarlo un siglo después.
Hay materiales que, además de tener un alto límite de elasticidad (resisten mucho), tienen un módulo de elasticidad relativamente bajo. Esto es súper interesante porque hace que las cosas se deformen mucho antes de romperse sin dejar de ser resistentes. Un ejemplo de un material así es la seda de araña. En base a estudios de gente que investiga este loco producto natural, se sabe que la tensión de rotura de la seda de araña puede llegar a 1550 MPa (megapascales, una unidad de presión). Esto implica que un cable del diámetro de un lápiz (7 mm) podría aguantar una carga de 5965 kg (!). O sea, podríamos colgar un cohete Saturn V (el que, entre otras cosas, nos hizo llegar por primera vez a la Luna) de un cable de 15,5 cm. Eso es tener aguante.
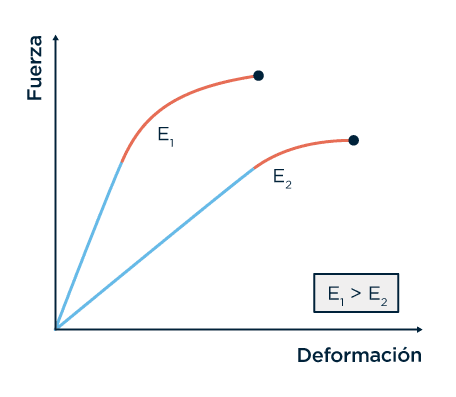
Representación de dos materiales con módulos de elasticidad diferentes.
A priori parecería algo malo que algo se deforme y rompa. Pero pensemos en cómo sería vivir en un mundo donde a las cosas no les pasara esto; no se podría abrir una cerveza porque ni la tapita ni la chapa de la lata se deformarían; tocar la guitarra sería imposible porque las cuerdas no vibrarían; los huevos se volverían una amenaza letal para los recién recibidos; dormir en el colchón, un castigo; hacer bungee jumping sería una muy mala idea; y esos zapatos nuevos divinos no van a ceder jamás y los terminaré usando de maceta.
Todo esto del estudio de las deformaciones es una herramienta súper potente que, combinada con algunas otras, nos da la oportunidad de usar lo poquito que sabemos de ella para solucionar problemas de todos los días. No sólo es aplicable a no reventarte los dedos cuando estas aburrido jugando con la bandita. Sirve también para hacer cosas mucho más importantes como, por ejemplo, los análisis de impacto en coches para disipar energía en la deformación de la carrocería y aumentar así la seguridad de los pasajeros; el estudio de los suelos para que no se deformen mucho cuando le metemos un edificio encima; hacer que si se nos mueve el piso los edificios no se caigan. Y no nos olvidemos de los imprescindibles resortes que nos solucionaron desde el andar de los relojes hasta poder comerte un bache en el auto sin perder la columna vertebral.
El universo de las deformaciones es realmente enorme y podríamos estar horas hablando sobre las diferentes aplicaciones de todos estos temas, pero no quiero estirarla mucho a ver si todavía se rompe.
Aclaración:
Pese a que el ejemplo principal de algo deformable para hablar de la Ley de Hooke fue una bandita elástica, éstas no siguen estrictamente la Ley de Hooke. Las gomas y plásticos son materiales hiperelásticos que siguen un modelo Neo-Hookeano.
De todas maneras, a modo de ejercicio mental, es tremendamente útil usar las banditas elásticas de ejemplo. Por otro lado, hasta 1948 no se planteó la teoría Neo-Hookeana, así que trabajamos mucho tiempo pensando que las banditas elásticas sí siguen la Ley de Hooke.
El modelo Neo-Hookeano considera, entre otras cosas, disipación de calor en la deformación. El modelo de Hooke es una aproximación lineal y elástica, mientras que el Neo-Hookean es una aproximación no lineal, por ende, más compleja, y dentro de su rango de aplicación, más precisa.



