San Juan y Boedo antiguo y todo el cielo,
Pompeya y, más allá, la inundación,
tu melena de novia en el recuerdo,
y tu nombre flotando en el adiós…
Homero Manzi – Aníbal Troilo
¿Podrán las computadoras componer un tango? O, incluso, más ambicioso: ¿podrán algún día disfrutarlo? Con los avances en inteligencia artificial volvieron a surgir preguntas que ya estaban desde el nacimiento de la computación. Alan Turing sostenía que las computadoras podrían producir y apreciar arte, pero un arte que ellas disfrutaran en sus propios términos y nosotros no tuviéramos por qué compartir. Uno de los autores de ciencia ficción más renombrados, Philip K. Dick, se preguntaba si los androides sueñan con ovejas eléctricas (la novela con ese nombre dio nacimiento a la película Blade Runner). Pero antes de plantearnos si una computadora puede igualar a Manzi y Troilo en la composición del tango Sur (el cientista de datos Germán Rosatti se encuentra investigando esos asuntos), en las palabras que siguen nos contentamos con intentar abordar una pregunta acaso más modesta, pero igualmente necesaria en el trayecto de soñar con una tostadora con deep learning que llore con Balada para un Loco: hoy nos preguntamos cómo sabe la computadora siquiera dónde queda San Juan y Boedo.
Los alemanes pueden disfrutar de El Quijote, pero primero necesitan traducirlo al alemán (o aprender español). Con las computadoras ocurre algo similar, necesitan traducir las cosas a su lenguaje: la matemática. La solución que hoy utilizan la mayoría de las computadoras para traducir San Juan y Boedo, o cualquier ubicación espacial, al lenguaje matemático es usar un par de ejes de coordenadas cartesianos. Estos ejes muestran la latitud y longitud de un punto: una coordenada o par de coordenadas. En nuestro caso, la esquina de San Juan y Boedo corresponde a las (al menos para mi oído humano) infinitamente menos musicales coordenadas: -34.625422, -58.416125.
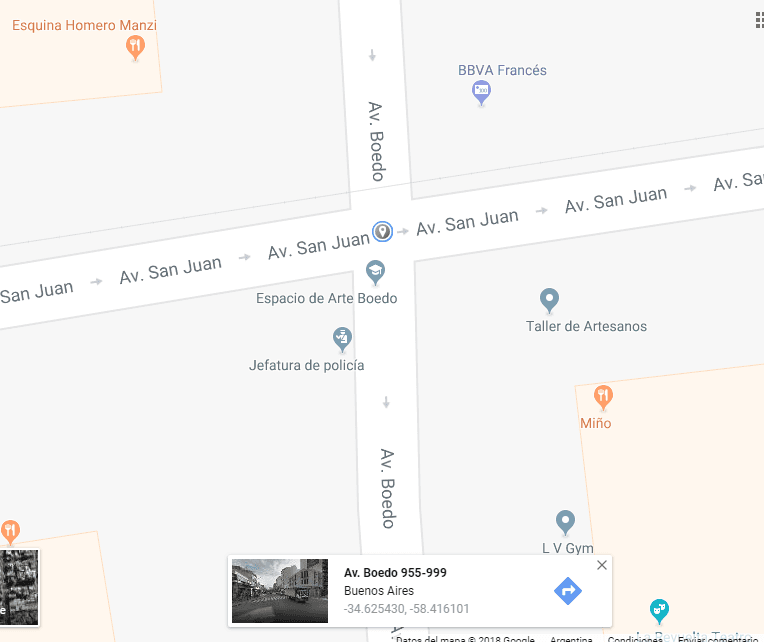
-34.625422, -58.416125 antiguo y todo el cielo, Pompeya y, más allá, la inundación.
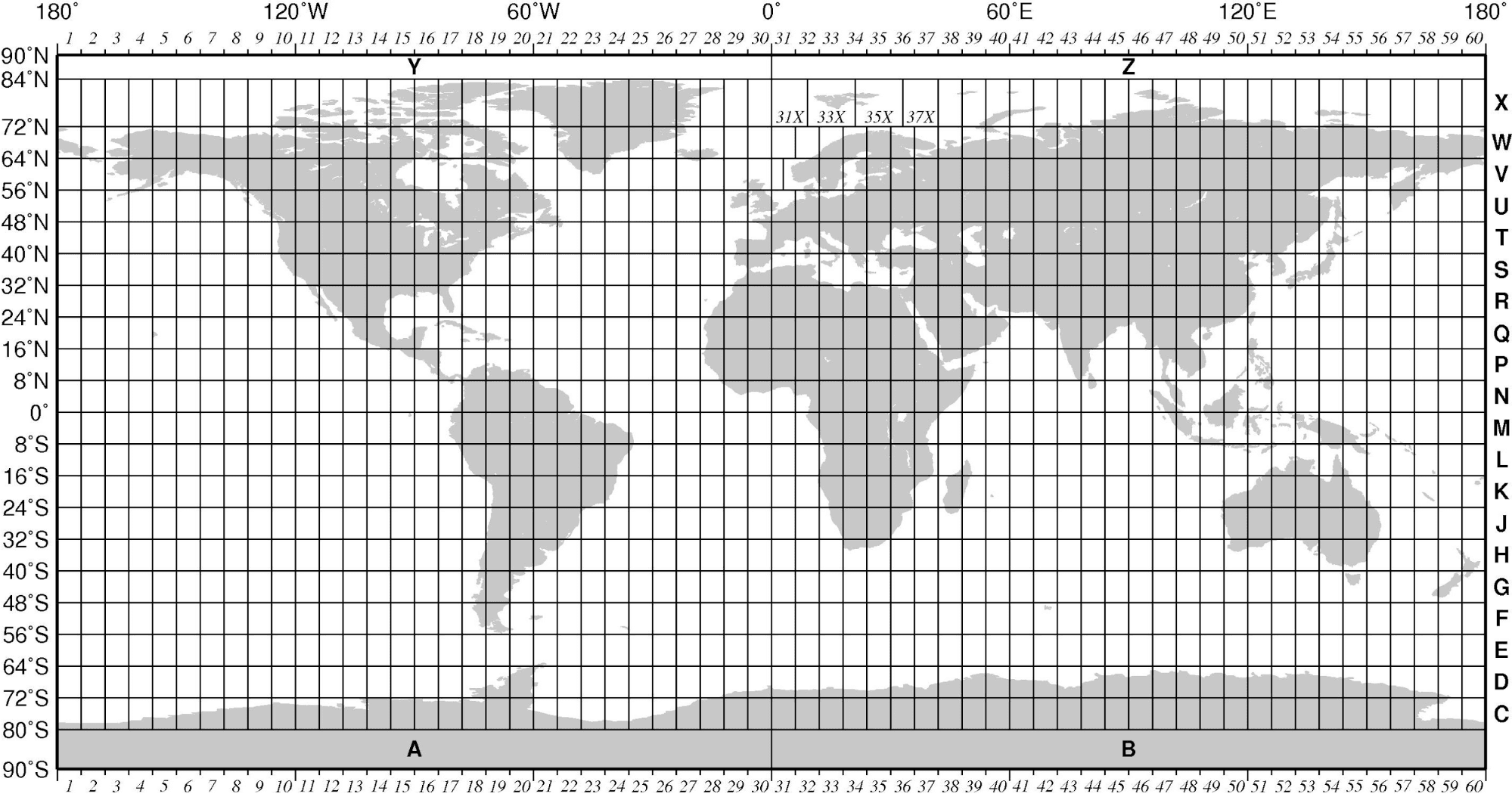
Longitud y latitud: el par de coordenadas
Este par de coordenadas incluye también signos que nos indican que la esquina de San Juan y Boedo está al sur (-) del Ecuador y al oeste (-) del Meridiano de Greenwich (el cruce de ambos sería la coordenada 0,0, el ombligo del mundo para nuestros GPSs). Se utilizan los grados porque el planeta Tierra es un geoide con tres dimensiones y, para hacer las cosas más sencillas, nosotros lo reducimos a sólo dos dimensiones. Este truco se realiza por un proceso apasionante que se llama Sistema de proyección de coordenadas. Hay muchas proyecciones, algunas de ellas muy divertidas, pero no es lo que queremos contar en esta oportunidad.
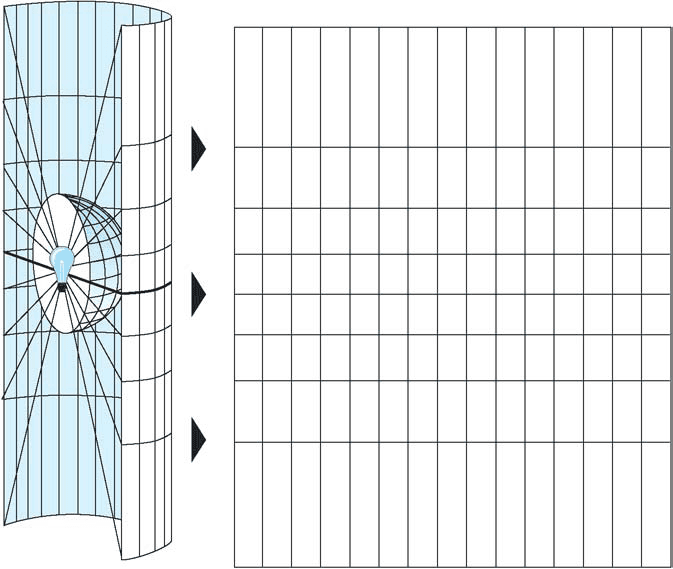
Acá podemos ver cómo pasar de una esfera (geoide, pero se entiende) a un plano, así como las ‘deformaciones’ que este proceso genera en nuestra percepción de la superficie de nuestros continentes.
Ahora, si bien -34.625422, -58.416125 es San Juan y Boedo, también lo es -34.625421, -58.416124. Y -34.625423, -58.416126 (nótese que estoy cambiando solamente el dígito final de cada cifra, lo cual en el mapa equivale a desplazarse apenas un poquito). Porque las esquinas de una ciudad son más bien áreas y las computadoras no son buenas lidiando con la ambivalencia. Necesitan índices o identificadores (IDs) únicos para encontrar las cosas. Algo así como un pasaporte para cada calle. A nuestro modo, los humanos también. Hay una sola Avenida San Juan en la ciudad de Buenos Aires. Como hay una sola Avenida Boedo. Si no, sería muy problemático encontrarse con amigos en San Juan y Boedo. Un grupo iría a una esquina, otros a otra, o algunos perdidos en el caso de que las avenidas San Juan y Boedo alternativas nunca se crucen. Las coordenadas no tienen este problema. Pero si yo estoy parado en la esquina del Bar de Homero Manzi (-34.625422, -58.416125) y mi amigo en la esquina en diagonal (-34.625421, -58.416126), nuestras coordenadas van a ser diferentes. Si les tocase a nuestros celulares y sus GPS decir si nos encontramos o no, la respuesta sería que no. Porque nuestras coordenadas son diferentes, a pesar de que estamos en la misma esquina.
Echando mano al teorema de un griego que nació hace aproximadamente unos 2500 años, podemos saber la distancia entre dos puntos cualquiera en un plano, como por ejemplo el celular de mi amigo y el mio. Valiéndonos de Pitágoras podemos calcular esta distancia, que toma el nombre de otro griego, Euclides, que definió algunas de las propiedades básicas de la geometría en 2 dimensiones (recordemos que la latitud y longitud son una proyección de nuestro mundo tridimensional a 2 dimensiones). De allí que se llame distancia euclidiana. Simplemente reemplace X por longitud e Y por latitud y tendrá una distancia.
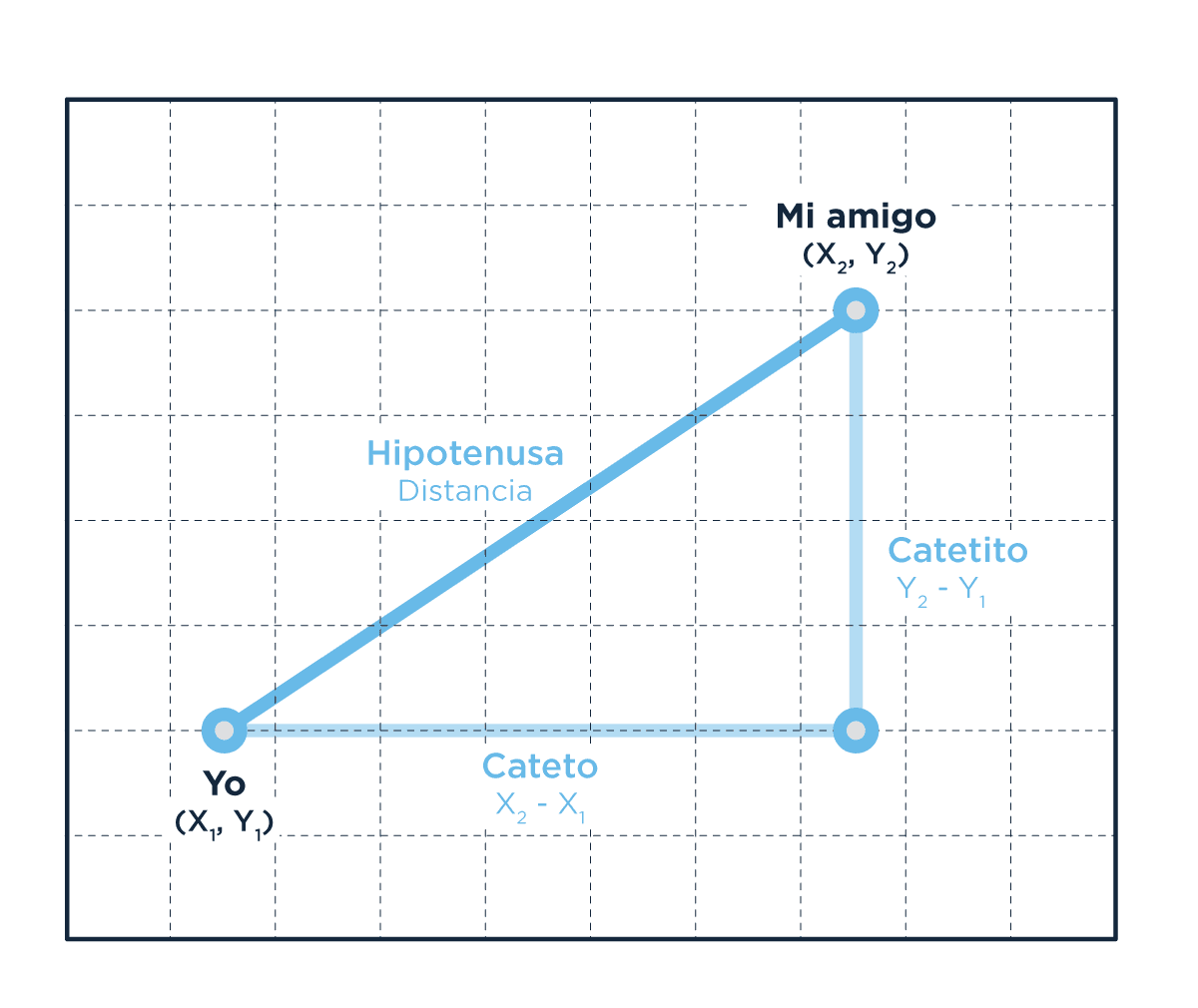
-Amor, sí, te estoy esperando en (x2-x1; y2-y1), deberías estar cerca, te veo recorriendo la distancia euclidiana. No, pará. ¿Qué querés decir con que esto no es euclidiano? QUE DOS RECTAS PARALELAS EN EL INFINITO, ¿¿¿¿QUÉ????
Entonces, si esa distancia es menor a un rango que consideramos tolerable (supongamos que, sin mucha miopía mediante, 10 metros es suficiente para que nos veamos), nuestros celulares nos avisarán que nos encontramos. Cómo podemos calcular una distancia en metros cuando nuestras unidades están en grados es una pregunta que también responde el apasionante (bueno, ‘apasionante’) mundo de las proyecciones de coordenadas. Existen proyecciones que trabajan midiendo la distancia en metros al Ecuador y a Greenwich.
Si bien esto parece una pregunta tonta, dado que mi amigo y yo podemos resolver este problema porque la gente se viene encontrando desde antes de las computadoras (de hecho, se habrán tenido que encontrar más de una vez para poder hacer las computadoras en primer lugar), cada vez más este tipo de decisiones va a caer en manos de computadoras que no tienen la inteligencia humana para resolverlo. Hoy pedimos un transporte usando una app, que del otro lado es leída por un humano capaz de zanjar el pedacito ambiguo que hay entre estar en la esquina de Ciudad de La Paz y Monroe y estar en la esquina de Ciudad de La Paz y Monroe, donde está el kiosko ese, te das cuenta porque hay una señal de no doblar rota en la punta. Pero esta diferencia supone la necesidad (todavía) de un conductor humano, y todo indica que muchos de los procesos urbanos cotidianos de hoy en día estarán cada vez más mediados por el uso de computadoras, robots y drones. Y como muchos de los procesos urbanos suceden en este espacio es muy importante encontrar una forma de modelarlo para que las computadoras puedan interpretarlo y darle sentido (u operar como si tuviese sentido, para circunvalar una difícil conversación sobre qué es sentido y cómo y quién puede darlo).
Todos los que nos detuvimos complicados frente a Google Maps sabemos que la computadora no sabe de entrada si al tipear ‘Sarmie..’ hablamos de Sarmiento la calle, la avenida o la Avenida Fragata Sarmiento. Tampoco si es la Sarmiento de CABA o de Avellaneda. Las computadoras necesitan IDs únicos. Por supuesto, además, esos IDs necesitan ser universales. Muchas de las compañías que desarrollan estos equipos no pueden adaptarse demasiado a las particularidades de las calles de cada región. Debe ser lo más generalizable posible. Por eso es que hoy en día existe una búsqueda, por parte de numerosas proyectos en curso, de una nomenclatura única amigable para las computadoras. Cualquier equipo puede estar integrado con un GPS y reportar el par ‘Latitud – Longitud’ permanentemente. Pero, como vimos, es necesario poder dar un contexto más inteligible a ese par.
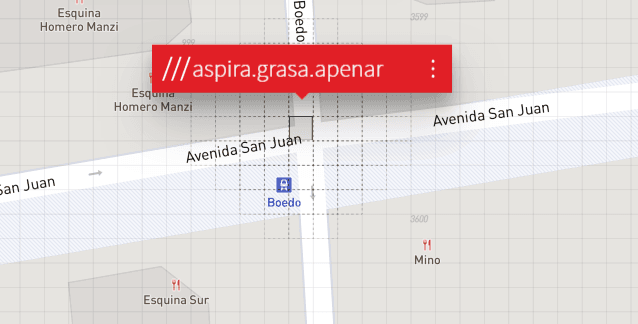
What 3 words (piedra.papel.tijera)
Un proyecto que intenta dar una respuesta a esto es What 3 words (‘cuáles tres palabras’), el cual divide al mundo en una grilla con celdas de 3 x 3 metros y les asigna 3 palabras al azar a cada una. Algo así como el alias del CBU de nuestras cuentas bancarias, pero para pedacitos de la Tierra. Hay que reconocer que esto aporta algo de color al asunto, y lo aleja de los largos y fríos números de las coordenadas. Sin embargo, sigue sin resolver el problema de fondo ya que no tenemos cómo saber la distancia a la que está ‘aspirar.grasa.apenar’ de ‘crio.cenamos.alarmas’, y ni hablar de otra información relevante para los humanos que navegamos esos trayectos, como cuál es la próxima esquina con mano a la derecha, o si estoy en un sendero donde pueden circular bicicletas o sólo peatones.
El mapa del mundo: Open Street Map
En el cuento ‘El rigor de la ciencia’, Borges imaginaba el mapa de un Imperio que llegaba a tener una escala 1:1, es decir, que una hoja de 1 x 1 metro del mapa, representaba un espacio de 1 x 1 metro del Imperio. El mapa de la baldosa donde mi gato duerme la siesta, sería un dibujo de mi gato. Mapa práctico, si los hay. Ideal para la mochila de cualquiera que quiera llevar encima un mapa de su mochila.
Afortunadamente, la posibilidad de crear un mapa del mundo, a cualquier escala que sea necesario, cambió con el desarrollo de la computación en general y con el nacimiento del proyecto Open Street Map (Mapa Abierto de Calle, OSM por sus siglas en inglés) en particular. OSM es un esfuerzo colaborativo mundial que se basa en la filosofía del software libre. Cuenta la leyenda (que hay que tomar como leyenda hasta que esté chequeada, pero que en este caso, como no impide que nadie se vacune, bien podemos aceptar como leyenda) que OSM nace como producto de la sana rebeldía de un británico contra la obligación de pagar a la reina por cada mapa que se compraba. En 2004, este estudiante de ciencias de la computación de Gran Bretaña, Steve Coast, dio nacimiento a OSM, el proyecto para mapear al mundo entero, donde todos y cada uno de sus habitantes pueden colaborar para mapear su calle, esquina, barrio, pueblo, ciudad, país, de un modo totalmente libre, abierto, colaborativo y en perpetua corrección como lo es Wikipedia, gracias a lo cual (y no a pesar de) es muy confiable.
OSM satisface algunas de las necesidades de las computadoras para conocer el espacio urbano. Por un lado es universal, hay mapas de OSM para todas las ciudades del mundo. Al mismo tiempo mapea edificios, plazas, bares, todo un conjunto de elementos que hacen a las ciudades. Pero una de las características más interesantes es lo que hace con las calles y esquinas. Estas son muy importantes para el espacio urbano. Podríamos incluso decir que el espacio urbano está estructurado por veredas, calles y esquinas. La periodista newyorkquina Jane Jacobs, que fue una de las inspiradoras del nuevo urbanismo, solía decir “Las calles y sus aceras, los principales lugares públicos de una ciudad, son sus órganos más vitales. ¿Qué es lo primero que nos viene a la mente al pensar en una ciudad? Sus calles. Cuando las calles de una ciudad ofrecen interés, la ciudad entera ofrece interés; cuando presentan un aspecto triste, toda la ciudad parece triste”.
Lo que OSM hace para cada calle y esquina es asignarle un número único, el DNI de las calles y esquinas. Al mismo tiempo nos dice si esa vía es peatonal, para bicicletas, compartida, para autos, únicamente para buses, etc. Nos dice qué y quién puede circular por ahí. Pero el aporte fundamental de OSM es que ofrece la materia prima para construir un modelo de nuestras veredas, calles y esquinas que sea fácil de analizar para las computadoras, que lo traduzca a su idioma. Al identificar cada esquina de manera única y definir una calle-vereda como una unión de esquinas (y darle también un ID único), ofrece los elementos fundamentales para construir un modelo matemático que represente el entramado urbano en su complejidad y sea asimilable para las computadoras: un grafo.
Los grafos: las calles y esquinas como nodos y arcos
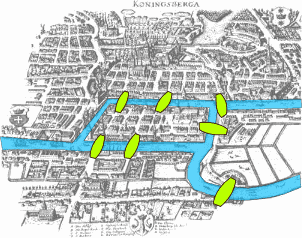
Tenemos el concepto de grafo justamente porque el matemático suizo Leonhard Euler se cruzó con un problema de naturaleza urbana y, para resolverlo, tuvo que inventar (¿o descubrir?) los grafos. Ocurre que Kaliningrado (Rusia), originalmente Königsberg, es famosa por sus siete puentes que unen ambos márgenes del río Pregel con dos de sus islas. Dos de los puentes unen la isla mayor con la margen oriental y otros dos con la margen occidental. La isla menor está conectada por un puente a cada margen y el séptimo puente une ambas islas. El problema planteaba lo siguiente: ¿es posible dar un paseo comenzando desde cualquiera de estas regiones, pasando por todos los puentes, recorriendo sólo una vez cada uno y regresando al mismo punto de partida? Podríamos publicar la respuesta, podría googlearse, pero sugerimos pasar unos minutos intentando y dibujando. Es una manera divertida de matar el tiempo (bueno, ‘divertida’). Aquí, el esquema:
Entonces Euler, para resolver esto, creó la idea de grafos: nodos o vértices unidos por arcos o aristas que expresan estos elementos y sus relaciones. Una idea que nace con un emplazamiento urbano real, pero que se abstrajo y se utiliza para muchas cosas. Por ejemplo, para expresar relaciones en redes sociales. Dos personas (nodos) se conocen entre sí (hay una relación, un arco). O el nodo Agüero le pasó al nodo Messi la pelota 10 veces. Esos arcos a su vez pueden ser direccionados (Agüero le pasó la pelota a Messi en ese sentido, Messi le puede haber pasado a Agüero también en otro sentido) y tener diferentes valores (Messi se la pasó solamente 5 veces).
Si bien los grafos se usaron para todo tipo de aplicaciones, ahora podemos volver a usarlos para su primer uso: las ciudades. Las esquinas pueden funcionar como nodos y las veredas (y calles) como arcos. En una calle uno puede ir de un nodo (San Juan y Boedo) a otro (San Juan y Entre Ríos) en un sentido, pero no en otro porque San Juan sólo permite circular de Oeste a Este. O si uno circula en una calle de un sentido, pero sobre una ciclovía de dos sentidos, eso cambia. O en una avenida doble mano. Una vereda puede ser más ancha y más fácil de caminar (o una calle tener más carriles) para trasladarse de un nodo a otro. Todas estas propiedades son de enorme ayuda para convertir el problema del espacio urbano en algo que las computadoras puedan comprender en su lenguaje.
Mapas de grafos
Convertir un mapa de una ciudad en un grafo puede ser de mucha utilidad para resolver problemas cotidianos utilizando computadoras. Por ejemplo cómo voy de Córdoba y Estado de Israel a Scalabrini Ortiz y Santa Fe, recorriendo el camino más corto. Para eso existe una solución que se denomina el algoritmo de Dijkstra, por un cientista de la computación de los Países Bajos que desarrolló esta solución en 1959.
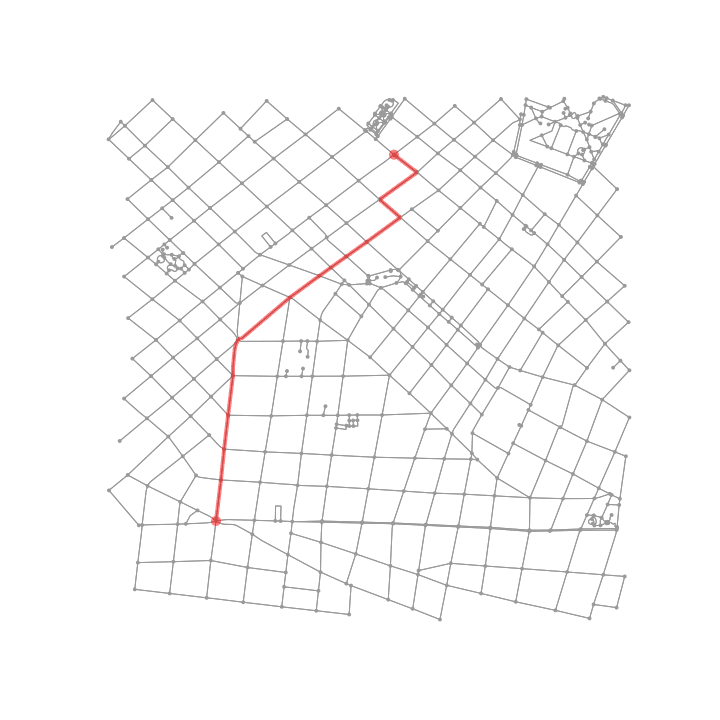
La otra opción es tomarse el 160.
El camino más corto es Gascón, Julián Álvarez, Güemes, Aráoz, Santa Fe. Se eligió siguiendo el camino con la menor cantidad de cuadras posibles. Se puede ser más preciso y no asumir que todas las cuadras miden lo mismo en metros. Si agregamos a nuestro grafo la información del largo de cada cuadra, podemos solucionar este problema indicando que el camino elegido sea el que nos haga caminar menor cantidad de metros (es decir, que minimice la cantidad de metros a recorrer).
Volviendo a la pregunta original ¿cómo sabe la computadora dónde es la esquina de Estado de Israel y Córdoba? En este caso, la computadora identifica esa esquina como 195769564 (su ID). Y a Scalabrini Ortiz y Santa Fe como 92616223. Entonces, el recorrido ‘Gascón, Julián Álvarez, Güemes, Araoz, Santa Fe’ no es más que una secuencia de esquinas (o nodos), tremendamente difíciles de señalarle a un taxista, pero preciosas para su GPS:
[195769564,
81601542,
81601843,
89138852,
92611349,
4466582349,
181074112,
177162925,
92600036,
217886894,
191173207,
191173197,
107928845,
437539838,
92616223]
Si bien la mayoría de las veces que queremos ir de un lugar a otro pretendemos gastar la menor cantidad de energía posible (caminando la menor cantidad de metros), este no es siempre el caso. Si somos turistas podríamos querer recorrer el camino más ‘atractivo’. Entonces deberíamos agregarle a cada esquina ya no su largo en metros, sino la cantidad de fotos en Instagram tomadas en la latitudes y longitudes cercanas a esa cuadra. Y esta vez querríamos recorrer el camino que maximice esa cantidad.
Existen otros problemas tradicionales en este sentido. Imaginemos que somos un cartero chino (el problema se llama así pero, más allá de eso, creo que Borges lo habría titulado igual), tenemos un conjunto de manzanas para dejar nuestras cartas y tenemos que hacerlo recorriendo la menor distancia posible, pero siempre recorriendo todas las cuadras (no podemos no visitar una casa y dejarla sin correo). Si bien parece un problema abstracto alejado de nuestra realidad cotidiana, más aún por el nombre que lleva, también se podría llamar ‘el problema del basurero de Morón’, principalmente porque este método fue utilizado para optimizar la ruta de los camiones de recolección de residuos en dicho municipio.
Para reconocer estas esquinas de manera unívoca se utilizaron los IDs de Open Street Map. Esto permite resolver este problema para cualquier par de puntos en cualquier ciudad del mundo que tenga Open Street Map. Finalmente, para el ruteo, se utilizó un proyecto del urbanista Geoff Boeing llamado Osmnx.
Osmnx
Geoff trabajó en observar la complejidad de las ciudades, utilizando diversas métricas. Muchas de ellas vinculadas a la estructura en forma de grafos de las calles, veredas y esquinas de nuestras ciudades.

Imagen de una estructura espacial con un patrón fractal que se asemeja al plano de una ciudad (dividida en manzanas y dentro en parcelas) o a estructuras urbanas micro como la Torre Eiffel. Fuente
Para resolver este problema, tomó la información de OSM y una librería para grafos del lenguaje de programación Python (llamado en base al grupo cómico inglés Monthy Python) y creó Osmnx. Esta herramienta justamente nos permitió encontrar el camino más corto en el ejemplo anterior. También permite, por ejemplo, ver la orientación de las calles de las ciudades del mundo:
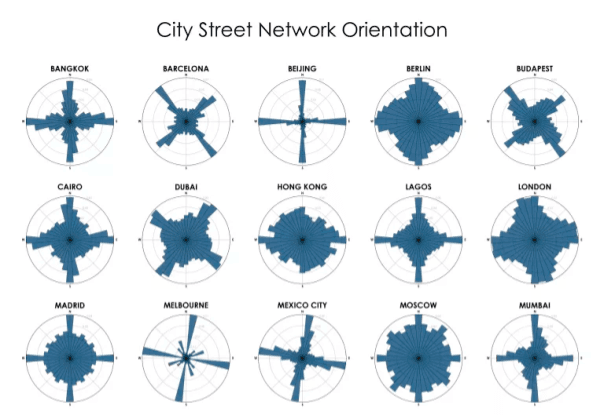
Orientación de las calles de diferentes ciudades del mundo. Buenos Aires no figura en esta imagen, pero la avenida Corrientes, por ejemplo, tiene sentido hacia el este. Callao al norte. ¿Los humanos construimos las ciudades y organizamos nuestras calles de acuerdo a los puntos cardinales? El investigador Geoff Boeing intentó dar una respuesta a esta pregunta.
Dada la búsqueda de universalidad de la metodología, se puede replicar para ciudades o barrios de cualquier ciudad del mundo.
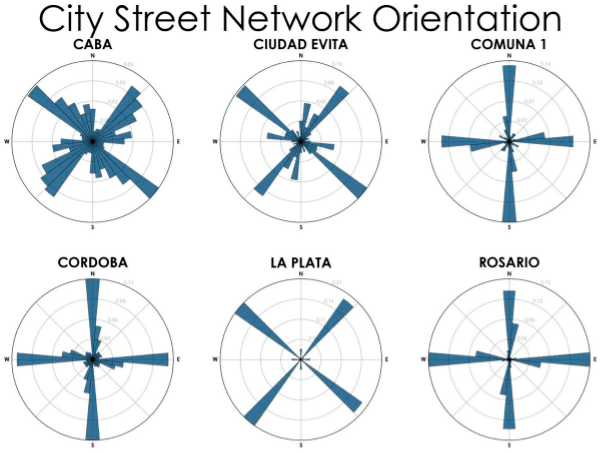
Método aplicado a ciudades y áreas urbanas de Buenos Aires. Mientras que la Capital Federal sigue un patrón aleatorio, la Comuna 1 (la más antigua de la ciudad) es la que más sigue la cuadrícula damera de la colonia y la menos azarosa. La Plata, la maravillosa ciudad planificada, parece dibujada por una computadora.
Osmnx nos permite convertir cualquier ciudad o parte de una ciudad en un grafo y tratarlo computacionalmente para aplicar los métodos ya conocidos de resolver problemas, o crear nuevos tomando las herramientas que los grafos en particular y las matemáticas en general nos brindan. También nos permite tomar cualquier par de coordenadas en latitud y longitud y convertirlo en un ID de OSM único. Retomando el ejemplo de San Juan y Boedo, sin importar qué coordenada reporte mi celular y el de mi amigo, al referenciarlo en un grafo de Osmnx siempre será el ID 206148601. Osmnx soluciona una parte muy importante del problema de brindar una nomenclatura urbana única amigable para las computadoras y con el mayor grado de universalidad posible. Pero tiene algunas limitaciones.
Shared Streets
Existe otro proyecto que nace con el objetivo explícito de brindar dicha nomenclatura: Shared Streets. No sólo para esquinas, sino también para cualquier punto sobre alguna calle o vereda. Para seguir con otro ejemplo tanguero, Corrientes 348 es un punto que se ubica sobre la vereda de la calle (arco) Corrientes, entre las esquinas (nodos) Corrientes y 25 de Mayo, y Corrientes y Reconquista. O, en lenguaje humano, Corrientes entre 25 de Mayo y Reconquista. Una vez que sabemos ese arco, nos ubicamos siguiendo la altura de la calle.

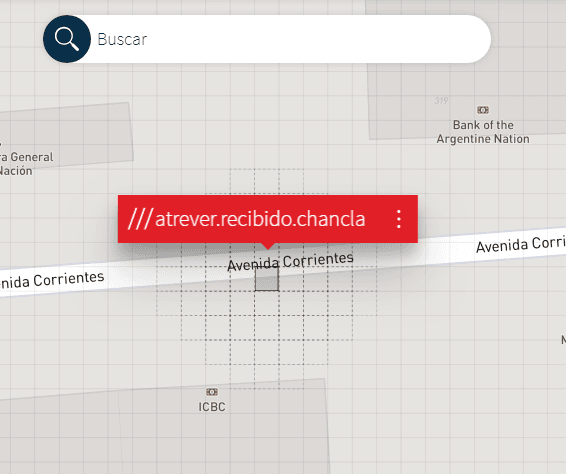
Las computadoras hacen esto de un modo similar utilizando el LRS (Linear Referencing System) o referenciamiento linear. Es muy similar a lo que hacemos con las alturas de las calles: el 400 de Corrientes significa más o menos a 4 cuadras de El Bajo o la Avenida Madero. El LRS funciona de manera similar: una dirección de Corrientes podría darse diciendo ‘parate en la esquina de Madero y Corrientes y caminá 420 metros’.
Este es el enfoque del proyecto Shared Streets. En primer lugar toma la idea de asignar un ID único a cada esquina (por ahora toma como información base los mapas abiertos de OSM, pero podría aplicarse el mismo método a mapas privativos que determinadas empresas o gobiernos no quieran compartir). Pero también lo hace para cada segmento de calle. Es decir, no sólo provee IDs únicos para las esquinas Corrientes y 25 de Mayo y Corrientes y Reconquista, provee también un ID único para la cuadra de Corrientes entre esas esquinas. Para Shared Streets, Corrientes entre 25 de Mayo y Reconquista equivale a bd98539adc529efc73870fcf6508c88b. Este ID es un hash (una cadena de caracteres única) que identifica cada segmento de calles en todas las ciudades del mundo. Por más que en alguna ciudad del mundo existe otra Corrientes, entre otra 25 de Mayo y otra Reconquista, no hay posibilidad de confusión. Cuenta otra leyenda, tan verídica como cualquier leyenda, que de hecho Corrientes 348 es una dirección en Montevideo (de donde es oriundo Carlos César Lenzi, autor de la letra de ‘A media luz’), no en Buenos Aires. Si fuese un tango compuesto por una computadora, no habría lugar a estas ambigüedades que son, al fin y al cabo, la materia prima de las leyendas.
Gracias a esto, podemos tomar montones de puntos de coordenadas geográficas que diferentes dispositivos con GPS arrojan por millones y ordenarlas de manera práctica. A su vez, dicho orden no es puramente contingente o arbitrario cuando se trata de fenómenos urbanos que probablemente se encuentren estructurados por las calles, veredas y esquinas como puede ser todo lo que tiene que ver con el transporte. Si tenemos una nube de puntos de coordenadas de subidas y bajadas de taxis o vehículos compartidos, necesitamos empaquetar esa información en valores fijos.
Agrupar así estos puntos permite realizar el análisis de concentración de ascensos y descensos de taxis de manera mucho más ordenada.
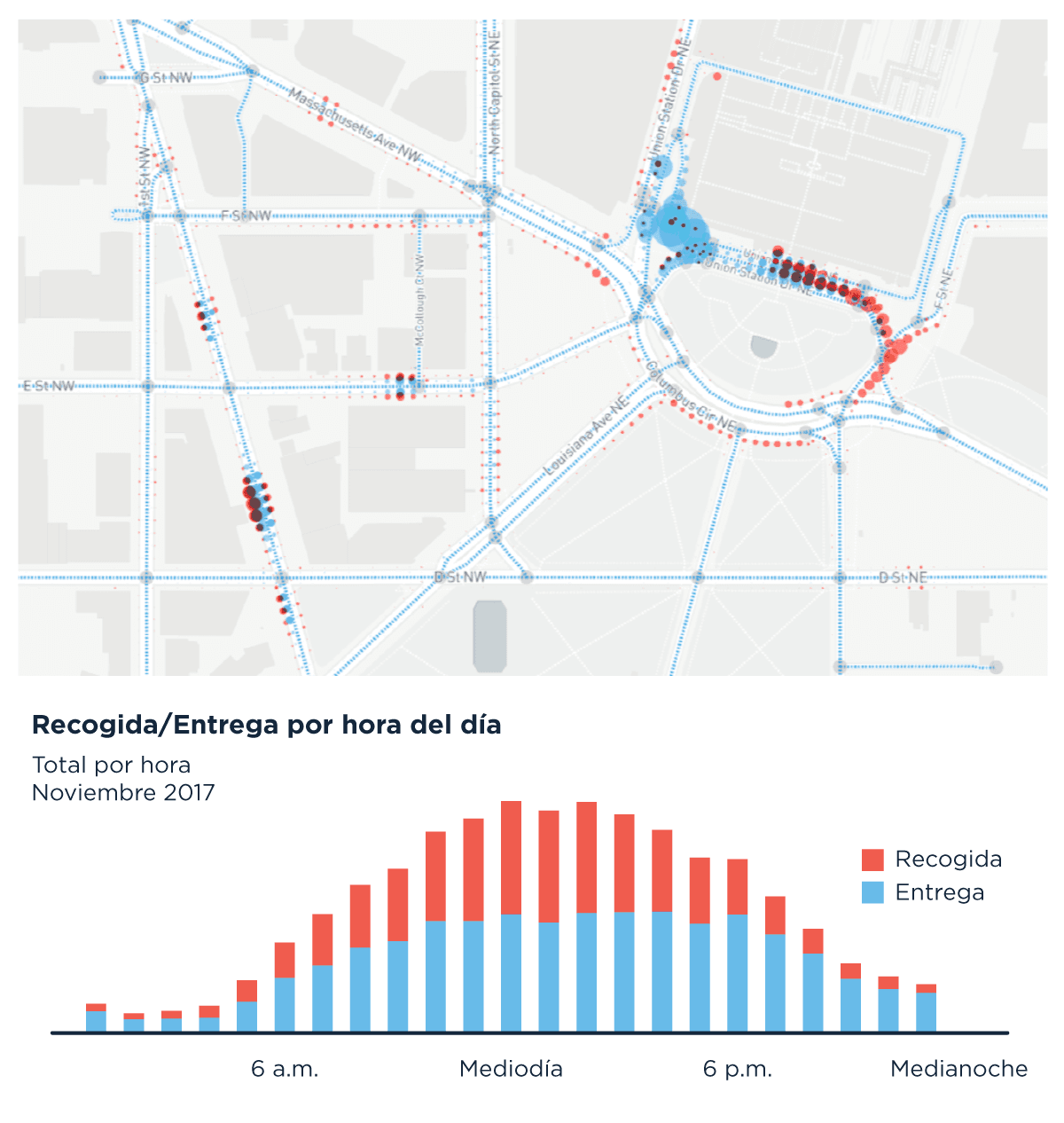
El enfoque de las grillas (como What 3 words) para para discretizar la nube de coordenadas de detención de taxis o buses es lo que podíamos hacer y nos permitiría detectar paradas populares. Pero esta forma de referenciar en el espacio tiene sus ventajas. En primer lugar referencia con una geografía real, no arbitraria como las grillas, pero que al mismo tiempo estructura los procesos que estamos analizando. El mismo proceso podría hacerse para detectar lugares frecuentes de detección de colectivos, o segmentos de calle donde habitualmente hay más autos estacionados, con su información GPS.
Imaginemos las ciudades dentro de 20 años (20 años podrá ser nada para el tango, pero al ritmo de avance tecnológico actual, es más de lo que hace desde que tenemos Facebook, y somos testigos de ese impacto). Hay una buena posibilidad de que muchos trabajos humanos sean sustituidos por computadoras, droides, robots, drones o como quieran llamarlos. Muchos de esos trabajos suceden en el espacio urbano y no pueden trasladarse al mundo online de la nube e Internet de las Cosas. Entrega de paquetes, taxis, buses, robots policías (esto ya está sucediendo en partes de San Francisco, con sujetos demasiado parecido a los Dalecks de la serie británica Dr. Who).

¡Deténgase!, pero sobre la calle, por favor, que no puedo subir el cordón para arrestarlo.
Si un scooter eléctrico que recién dejamos en la vereda, necesita desplazarse por sí mismo a una terminal para cargar su batería, necesita saber con mucha precisión dónde está ubicado, en que vereda y como llegar. Un colectivo autónomo necesita calcular el tiempo de arribo a la siguiente parada e incluso prever cuanta gente esta ubicada en esa parada gracias a los celulares que están en ella usando una app de arribo predictivo de colectivos. Los autos autónomos necesitarán saber donde se puede estacionar sin tener que leer carteles que no siempre están, o no están claros.
La pregunta pendiente es si todo esto implica o no que las computadoras sepan dónde queda San Juan y Boedo, y aventuro que la respuesta es más bien un sí con algunos asteriscos. Uno que dice que, más bien, saben dónde queda pizza.birra.tango. Otro que rescata que pueden acercarnos a (-34.625422, -58.416125) y sus alrededores, con una noción más que aceptable de lo que ‘alrededores’ es. Uno más que dice que pueden decirnos con altísima confianza cuántas personas se tomaron un taxi desde la puerta o qué tan rebuscada es esa parte de la ciudad. O hasta uno final, de esos que hacen que miremos para adentro, que dice que sí, que lo saben perfectamente, pero a su manera, y que es fútil tratar de inferir lo que saben y no saben, por lo menos hasta que hayamos encontrado formas más precisas de definir cómo los que nos hacemos esa pregunta sabemos, o si estamos buscando entender nuestras propias ovejas eléctricas en los sueños de otros.